7 Multiplication Methods and Types for All Grades

If you want to learn how to multiply, you have come to the right place! You will find here seven different methods for multiplying numbers: skip counting, arrays, repeated addition, the long multiplication algorithm, lattice multiplication, the grid method, and the drawing lines. These methods will help you solve any multiplication problem with ease and confidence.
Multiplication is one of the most important and useful skills in math. It helps us find the total number of items in equal groups, compare quantities, and solve problems from easy to difficult. But how can we teach multiplication to students of different grades and abilities? Here are multiplication methods and types for all grades, with some of the best multiplication strategies that build fluency and understanding.
-
Best multiplication strategies that build fluency
Multiplication is a fun and useful skill that can help you solve many kinds of problems. But how can you become fluent in multiplication and remember all the facts quickly and accurately? Here are some of the best strategies that can help you build your multiplication fluency:
Use skip counting
-
Skip-count by fives
Print it... -
Counting by 10's

Print it... -
Skip counting is when you count by a certain number, like 2, 3, 4, etc.
For example, to multiply 5 x 6, you can skip count by 5 six times: 5, 10, 15, 20, 25, 30.
Skip counting helps you see the patterns and relationships between numbers and makes multiplication easier.
Solve it with Arrays
-
Skip-count by fives

Print it... -
Counting by 10's

Print it... -
Arrays are arrangements of objects in rows and columns that show the product of two numbers.
For example, to multiply 4 x 3, you can make an array of 4 rows and 3 columns of dots:
Arrays help you visualize multiplication and see how it is related to addition and area.
-
Skip-count by fives
-
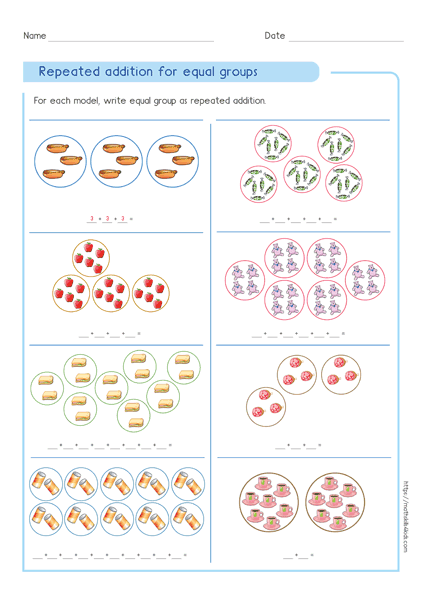
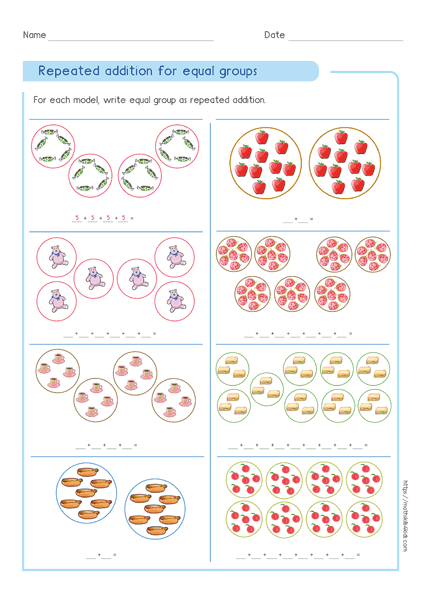
Repeated addition method
The repeated addition method is the simplest way to multiply. You just add the same number to itself as many times as the other number.
For example, to multiply 4 by 4, you add 4 four times: 4 + 4 + 4 + 4 = 16.
This method works well for small numbers or multiples of ten.
-
Long multiplication method
The long multiplication method is the most common way to multiply. You write the numbers vertically, one above the other, and line up the place values. Then you multiply each digit of the bottom number by each digit of the top number, starting from the right. You write the partial products below the line and add them up to get the final answer.
Area model or Grid method
The area model or Grid method is a way to multiply that uses a grid to break down the numbers into hundreds, tens, and ones. You write the numbers along the top and side of the grid, and then fill in each cell with the product of the corresponding digits. Then you add up all the cells to get the final answer.
-
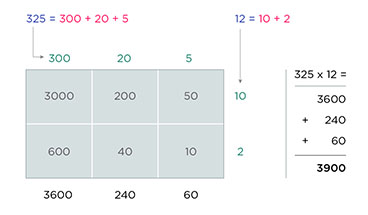
Example of multiplication with area model 325 x 12 -
For example, to multiply 325 by 12, you do this:
- Write 325 as 300 + 20 + 5 and 12 as 10 + 2.
- Draw a rectangle and divide it into four smaller rectangles. Label the length of the big rectangle as 300 + 20 + 5 and the width as 10 + 2.
- Find the area of each smaller rectangle by multiplying the length and width. For example, the area of the top left rectangle is 300 x 10 = 3000.
- Add up the areas of all four smaller rectangles to get the final answer. The areas are 3000, 600, 50, and 10. So, 325 x 12 = 3000 + 600 + 50 + 10 = 3900.
-
Chinese multiplication using lines and dots or drawing lines method
Chinese multiplication using lines and dots or the drawing lines method is a way to multiply that uses lines and dots to represent the numbers. You draw lines for each digit of the first number and dots for each digit of the second number. Then you count how many intersections there are in each place value and write them down.
For example, to multiply 325 by 12, you do this:
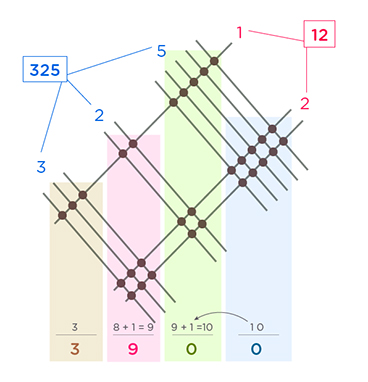
Example of multiplication with drawing lines method 325 x 12
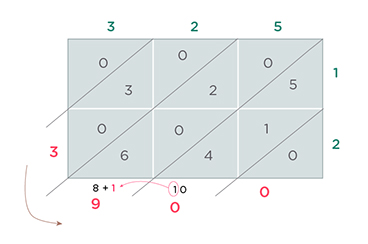
Lattice multiplication method or the Chinese long multiplication method
The lattice multiplication method, or the Chinese long multiplication method, is based on a simple idea: you can break down any number into its digits and then multiply them separately. For example, if you want to multiply 325 by 12, you can write them as 300 + 20 + 5 and 10 + 2. Then you can multiply each pair of digits and add them up. Sounds easy, right?
But how do you keep track of all the digits and places? That's where the lattice comes in.
A lattice is a grid of squares with diagonal lines inside. You write one number along the top and the other along the right side of the lattice. Then you fill in each square with the product of the corresponding digits. You write the tens digit above the diagonal and the ones digit below it. Like this:
Multiplication facts families
Multiplication facts families are groups of related multiplication and division facts that use the same numbers. For example, the facts family for 2, 4, and 8 is: 2 x 4 = 8, 4 x 2 = 8, 8 ÷ 2 = 4, and 8 ÷ 4 = 2. Facts families help you remember multiplication facts by showing how they are related to each other and to division.
Multiplication tricks and mnemonics
-
Tricks and mnemonics are clever ways to remember multiplication facts by using patterns, rules, rhymes, songs, stories, or images.
For example, to multiply by 9, you can use your fingers: hold up both hands and put down the finger that corresponds to the number you are multiplying by.
The number of fingers on the left is the tens digit, and the number of fingers on the right is the ones digit.
For example, to multiply 9 x 4, put down your fourth finger from the left: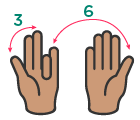 .
. You have three fingers on the left and six fingers on the right, so the answer is 36. Tricks and mnemonics help you remember multiplication facts by making them fun and memorable.
These are some of the best strategies that can help you build your multiplication fluency. Try them out and see which ones work best for you. Remember to practice regularly and have fun with multiplication!
- To multiply by 5, divide the number by 2 and then add a zero at the end. For example, 5 x 16 = (16 / 2) x 10 = 80.
- To multiply by 11, write the first and last digits of the number and add them in between. For example, 11 x 23 = write 2 and 3 and add them between 2 + 3 = 5. So, 11 x 23 = 253. If the sum of the digits is more than 9, then carry over the extra digit to the left. For example, 11 x 68 = write 6 and 8 and add them between 6 + 8 = 14. So, write 4 in between and carry over the extra 1 to the left: 11 x 68 = (6 +1)48 = 748.
- To remember the multiplication facts for numbers from 1 to 10, you can use some catchy phrases or rhymes that start with the same sound as the product. For example, for 6 x 6 = 36, you can say "six times six is thirty-six". For 7 x 7 =49, you can say "seven times seven is a fine forty-nine". For 8 x 8 =64, you can say "eight times eight fell on the floor and picked up sixty-four". For 9 x9 =81, you can say "nine times nine is eighty-one". And for 10 x10 =100, you can say "ten times ten is a big fat hen".