Standard algorithm multiplication worksheets PDF
Standard algorithm for multiplication
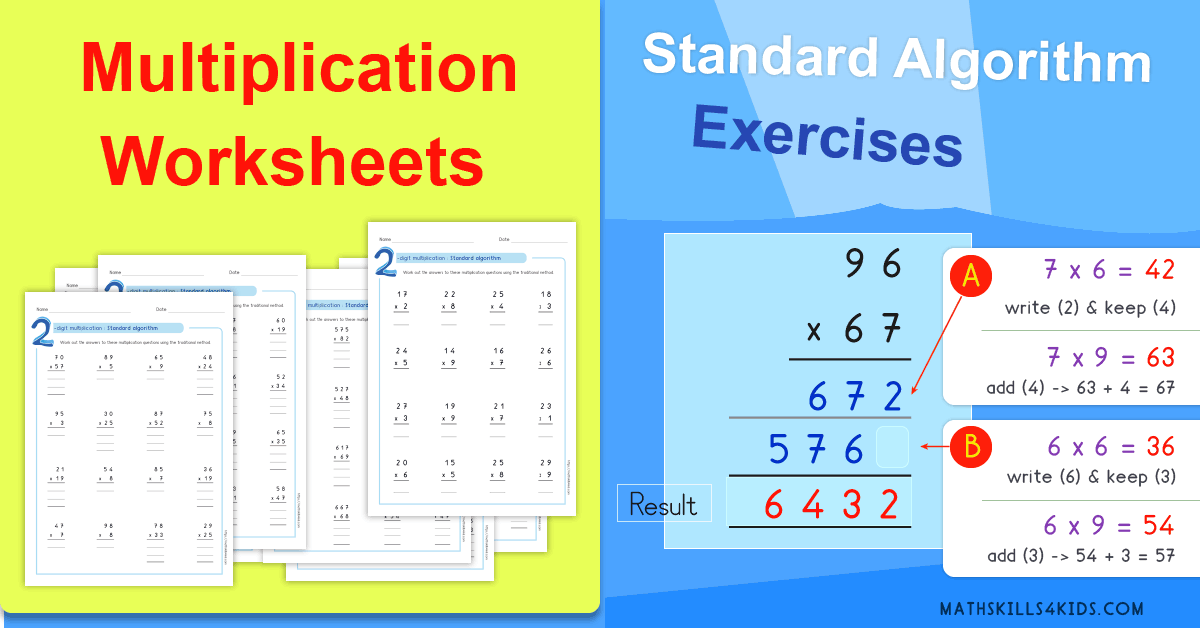
Standard algorithm multiplication worksheets PDF is another partial products method for multiplication. Here, you multiply ones and tens separately then and each partial products to find the final answer.
Amongst many multiplication methods, we also have the standard algorithm Multiplication Worksheets PDF. Standard algorithm is an old and one of the best methods of multiplying numbers with two and more digits. Multiplication here is done in parts.
This means that the ones and the tens are multiplied separately, then we add each partial product to obtain our final product.
 MORE MULTIPLICATION FACTS
MORE MULTIPLICATION FACTS
Multiplication Methods Activities
IMPORTANT FACTS ABOUT Standard algorithm method example
Standard algorithm for multiplication is a perfect tool for pencil and paper multiplication. It encourages kids to be able to find solutions for common mathematical problems.
No matter how large digits of a number are, standard algorithm helps you easily and quickly obtain correct answers with no stress. To this effect, our worksheets can boast of random exercises with multi-digit numbers ranging from 2 by 1 digits; 2 by2 digits; 3 by 2 digits; 4 by 2 digits and many lots.
Point to note - Examples of standard algorithm method for multiplication
Below are concrete examples of standard algorithm for multiplication, which you'll follow gradually the steps to arrive at the correct answer.
As we begin with our examples, you should take note that any time your answer is two digits long, carry the first digit above the number next to the top first right number, and place the second directly below the number on the row you were using to multiply.
Example 2. 2 digit multiplication: Standard algorithm | Multiplying 2 digit by 1 digit
Multiply 25 x 4
This is very easy to solve. It requires just the following steps.
Firstly, line up the numbers that you are multiplying, i.e. place the larger numbers on top and the smaller ones immediately below, following the places of tens and units. Remember to write the multiplication sign just below the first top number.
25
x 4
Secondly, we'll begin multiplying. Since there's just one multiplier, we multiply just once.
- 4 x 5 = 20 → (we write 0 below the first column, then we carry 2 over to the next column
- 4 x 2 = 8, (8 + the 2 we carried) = 10. We write 10 below the second column.
25
x 4
100
Hey! , this is just all. So fast and easy
This therefore shows that 25 x 4 = 100
Example 2. 3 digit multiplication: Standard algorithm | Multiplying 3 digit by 2 digit
Multiply 152 x 27
No stress. So simple. Just follow the steps below gradually.
In the first place, we line up our numbers with larger numbers at the top and smaller ones just below. Since we have up to 3 digits we'll place them in place of hundreds, tens and units.
152
27
Secondly, write the multiplication sign (x) right down below the top number, then draw a line below the bottom number, then we begin our first phase of multiplication
152
x 27
We'll begin by multiplying the number in the ones of the bottom, with all the numbers.
Of the top, beginning from the first number (7) to the last number (2)
- 7 x 2 = 14 → (we write 4 below the first column, then we carry 1 over to the next column
- 7 x 5 = 35 → (35 + the 1 we carried) = 36. We write 6 under the second column, and carry 3.
- 7 x 1 = 7 → (7 + the 3 we carried) = 10. We write 10 bellow the third column.
152
x 27
1064
Hmm wow! Good. Let's continue with our second phase of multiplication, this time with the number in the tenths place of the bottom, again, multiplying with all the numbers of the top.
Holaaa, before I forget, you gonna place a zero below the ones place of your new product of 10 6 4
i.e., below 4. The zero (0) is put there to show that you are moving on to multiply the tenths place value.
Okay, now let's begin our second phase of multiplication.
- 2 x 2 = 4 → (we write 4 to the left of 0, i.e. below the second column.
- 2 x 5 = 10 → We write 0 to the left of 4 and carry 1 over to the next column.
- 2 x 1 = 2 → (2 + the 1 we carried) = 3. We write 3 to the left of 0.
152
x 27
1064
+ 3040
4104
Finally, we add the top and bottom products
Bravoooooo! We have finished. It has been so perfect all along.
This will therefore mean that 152 x 27 = 4,104