5th Grade Geometry: Concepts, Questions, Examples, and Practice Problems
Hello, and welcome to this outstanding article about 5th Grade geometry. This article aims to take teachers' and parents’ teaching skills to the next level by providing key geometry concepts, questions, examples, and practice problems to uplift 5th graders’ spatial reasoning and problem-solving skills.
-
Learn and practice 5th Grade Geometry: A Step-by-Step approach with concepts, questions, examples, and practice problems.
Mathskills4kids.com is a fantastic website that makes math learning a beautiful experience. In this article, we will have fun while exploring 5th Grade geometric worksheets and activities. During this playful-learning experience, we hope to spark children’s curiosity and love to learn and practice 5th-grade geometry concepts regularly. Our step-by-step geometry learning approach includes concepts, questions, examples, and practice problems to help students master and apply geometric skills to real-world situations.
By the end of this article, Grade 5 students will better understand what geometry is, why it is important, and how it can help them think logically and creatively.
Geometry is the branch of mathematics that deals with shapes, sizes, positions, and dimensions of objects. Geometry is everywhere in the world, from the buildings we live in, to the patterns we see in nature to the art we create. Geometry helps us understand how things fit together, how they move, and how they change.
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
5th GRADE MATH TOPICS
- Number sense
- Addition and subtraction
- Multiplication
- Division
- Exponents
- Number theory
- Decimals
- Add & subtract decimals
- Multiply decimals
- Divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Mixed operations
- Problems solving
- Ratios and rates
- Percentages
- Money Math
- Number sequences
- Coordinate graph
- Variable expressions
- Data and Graphs
- Probability and statistics
- Telling time
- Unit of measurements
- 2D figures
- Triangles & quadrilaterals
- Symmetry & transformations
- 3D figures
- Geometric measurements
-
Buying is supporting us!
Buy Now...
-
-
Why learn geometry in 5th grade?
Geometry is an essential part of the 5th-grade math curriculum. Learning geometry in 5th grade will help children:
- Develop spatial reasoning skills, which are the ability to visualize and manipulate shapes and objects in their mind.
- Enhance problem-solving skills, which are the ability to find solutions to challenging situations using logic and reasoning.
- Improve communication skills, which are the ability to express ideas clearly and precisely using words, symbols, diagrams, and models.
- Prepare for higher-level math topics, such as algebra, trigonometry, and calculus, which rely heavily on geometric concepts and principles.
-
Basic geometric terms and definitions
Before diving into the topics of 5th-grade geometry, let's review some basic geometric terms and definitions that are essential to know. Here are some of the most common ones:
- Point: A point is a space location with no size or shape. We use a dot (.) to represent a point and a capital letter to name it. For example, A is a point.
- Line: A line is a collection of points that extends infinitely in both directions. We use a straight line (—) to represent a line and two points or a lowercase letter to name it. For example, AB or l is a line.
- Line segment: A line segment is part of a line with two endpoints. We use a straight line with two dots (••) to represent a line segment and two points to name it. For example, CD is a line segment.
- Ray: A ray is part of a line with one endpoint extending infinitely in one direction. We use a straight line with one dot (•—) to represent a ray and two points to name it. The first point is the endpoint, and the second is any other point on the ray. For example, EF is a ray.
- Angle: An angle is formed by two rays that share a common endpoint. We use an arc (∠) to represent an angle and three points or a capital letter to name it. The first and third points are on the rays, and the second point is the common endpoint. For example, ∠GHI or ∠J is an angle.
- Vertex: A vertex is the common endpoint of two or more rays that form an angle. For example, H is the vertex of ∠
- Plane: A plane is a flat surface that extends infinitely in all directions. We use a rectangle (▭) to represent a plane and three points or a capital letter to name it. For example, KLM or P is a plane.
- Polygon: A polygon is a closed figure of three or more line segments that do not cross each other. The line segments are called sides, and the points where they meet are called vertices. For example, △NOP is a polygon.
- Circle: A circle is a set of points all the same distance from a fixed point called the center. We use an oval (○) to represent a circle and one point or a lowercase letter to name it. For example, Q or r is a circle.
-
Types of angles and how to measure them
One of the main topics of 5th-grade geometry learning is angles. Angles are important because they help us describe how shapes are oriented and how they relate to each other. There are different types of angles based on their size or measure:
- Acute angle: An acute angle is an angle that measures less than 90 degrees. For example, ∠RST is an acute angle.
- Right angle: A right angle is an angle that measures exactly 90 degrees. We use a small square (□) to mark a right angle. For example, ∠UVW is a right angle.
- Obtuse angle: An obtuse angle is an angle that measures more than 90 degrees but less than 180 degrees. For example, ∠XYZ is an obtuse angle.
- Straight angle: A straight angle is an angle that measures exactly 180 degrees. It looks like a straight line. For example, ∠ABC is a straight angle.
To measure an angle, we use a tool called a protractor. A protractor is a semi-circle with degrees marked on it. To measure an angle with a protractor, follow these steps:
- Place the center of the protractor on the vertex of the angle.
- Align the baseline of the protractor with one of the rays of the angle.
- Read the number on the protractor where the other ray of the angle intersects the protractor. This is the measure of the angle in degrees.
-
Properties of parallel and perpendicular lines
Another topic of 5th-grade geometry is lines and how they interact. There are two particular types of lines that you need to know: parallel and perpendicular lines.
- Parallel lines: Parallel lines are lines that never intersect or cross each other. They are always the same distance apart. We use two arrows (//) to mark parallel lines. For example, AB // CD.
- Perpendicular lines: Perpendicular lines are lines that intersect or cross each other at right angles. We use a small square (⊥) to mark perpendicular lines. For example, EF ⊥
Parallel and perpendicular lines have some important properties that you need to know:
If two parallel lines are cut by a third line, called a transversal, then the angles formed by the transversal and the parallel lines have unique relationships. For example, in the figure below, AB // CD and EF are transversal.
- Corresponding angles: Corresponding angles are in the same position relative to the parallel lines and the transversal. They are congruent, which means they have the same measure. For example, ∠1 and ∠5 are corresponding angles, and ∠1 ≅ ∠
- Alternate interior angles: Alternate interior angles are between the transversal's parallel lines and opposite sides. They are also congruent. For example, ∠3 and ∠6 are alternate interior angles, and ∠3 ≅ ∠
- Alternate exterior angles: Alternate exterior angles are angles outside the parallel lines and on opposite transversal sides. They are also congruent. For example, ∠2 and ∠7 are alternate exterior angles, and ∠2 ≅ ∠
- Consecutive interior angles: Consecutive interior angles are between parallel lines and on the same transversal side. They are supplementary, which means they add up to 180 degrees. For example, ∠3 and ∠5 are consecutive interior angles, and ∠3 + ∠5 = 180°.
- Consecutive exterior angles: Consecutive exterior angles are angles outside the parallel lines and on the same transversal side. They are also supplementary. For example, ∠2 and ∠4 are consecutive exterior angles, and ∠2 + ∠4 = 180°.
- If two perpendicular lines intersect or cross each other, they form four right angles at their point of intersection. For example, in the figure below, JK ⊥ LM and N is their intersection point.
- All four angles formed by JK and LM are right angles. For example, ∠JNL is a right angle.
- All four angles have the same measure of 90 degrees. For example, m∠JNL = 90°.
-
Classifying triangles by sides and angles
Another important topic in 5th-grade geometry is classifying triangles by their sides and angles. Triangles are polygons with three sides and three angles. There are different ways to name triangles based on their characteristics.
By sides, we can classify triangles as:
- Equilateral: A triangle with three equal sides and three equal angles of 60 degrees each.
- Isosceles: A triangle with two equal sides and two equal angles opposite those sides.
- Scalene: A triangle with no equal sides and no equal angles.
By angles, we can classify triangles as:
- Acute: A triangle with all three angles less than 90 degrees.
- Right: A triangle with one angle of 90 degrees and two acute angles.
- Obtuse: A triangle with one angle more than 90 degrees and two acute angles.
We can also combine these classifications to name triangles more specifically. For example, an isosceles right triangle has two equal sides and one right angle. A scalene obtuse triangle has no equal sides and one obtuse angle.
To classify a triangle, we can use a ruler to measure the lengths of the sides and a protractor to measure the angles. We can also use some formulas to find the missing information. For example, the sum of the angles in any triangle is always 180 degrees.
So if we know two angles, we can find the third one by subtracting them from 180. Another formula is the Pythagorean theorem, which applies to right triangles. It states that the square of the hypotenuse (the longest side opposite to the right angle) equals the sum of the squares of the other two sides. So if we know two sides, we can find the third one using this formula.
-
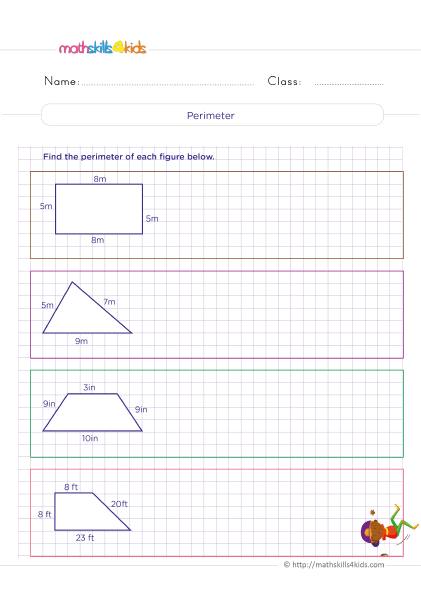
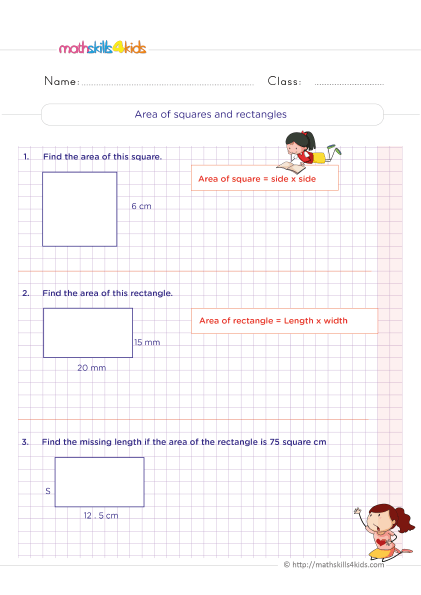
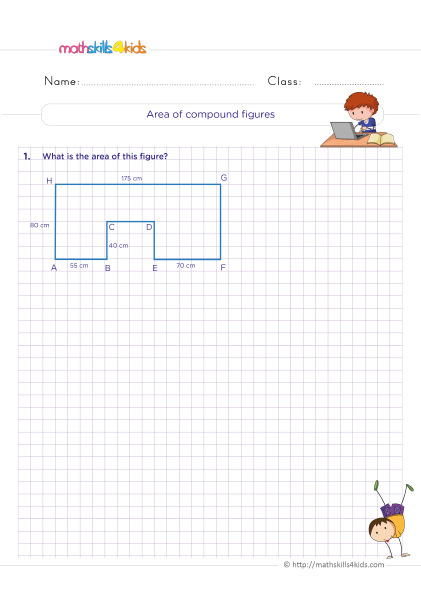
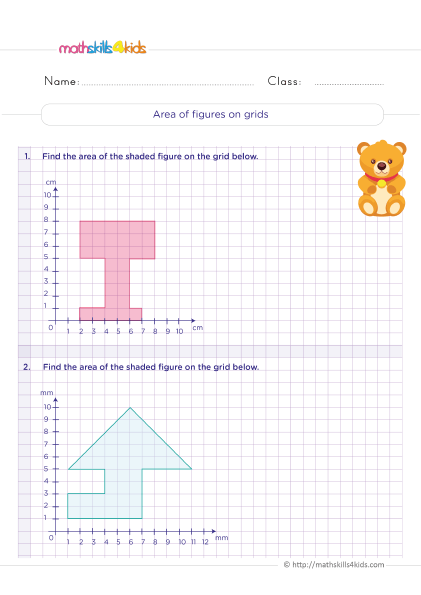
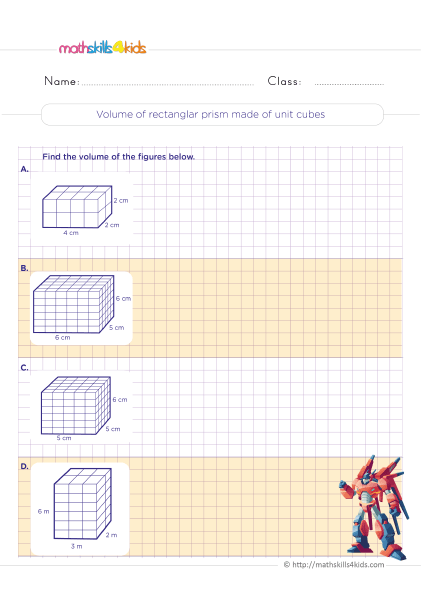
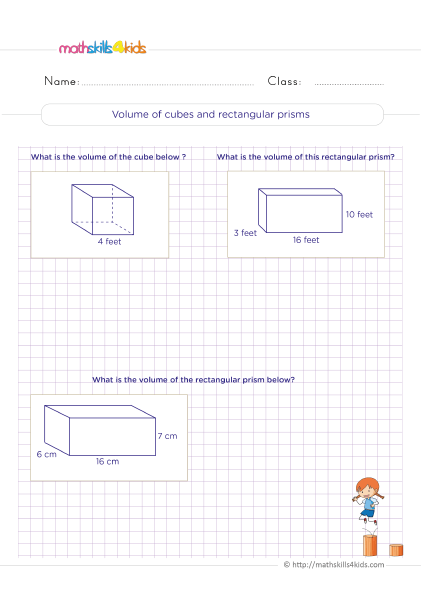
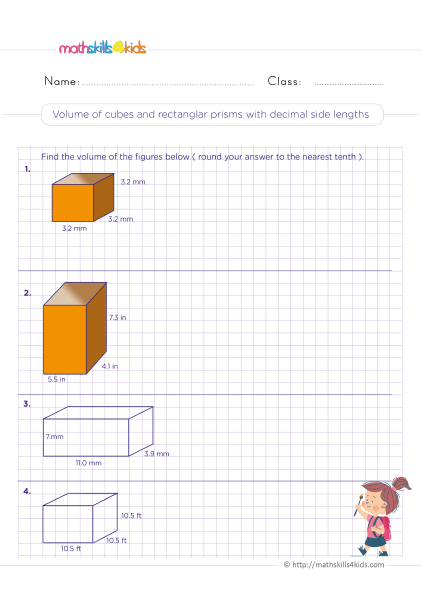
Finding the area and perimeter of polygons
Polygons are closed shapes with straight sides. Some common polygons are squares, rectangles, triangles, pentagons, hexagons, and octagons. To find the area and perimeter of polygons, we need to know some formulas and rules.
The area of a polygon is the amount of space inside it. The perimeter of a polygon is the total length of its sides. The formulas for finding the area and perimeter of some polygons are:
- Square: A square has four equal sides and four right angles. The area of a square is side times side or side squared. The perimeter of a square is four times side or side times four.
- Rectangle: A rectangle has two pairs of equal sides and four right angles. The area of a rectangle is length times width. The perimeter of a rectangle is two times length plus two times width or length plus width times two.
- Triangle: A triangle has three sides and three angles. The area of a triangle is base times height divided by two. The perimeter of a triangle is the sum of its three sides.
- Parallelogram: A parallelogram has two pairs of parallel sides and four angles. The area of a parallelogram is base times height. The perimeter of a parallelogram is two times base plus two times side or base plus side times two.
- Trapezoid: A trapezoid has one pair of parallel sides and four angles. The area of a trapezoid is base one plus base two divided by two times height. The perimeter of a trapezoid is the sum of its four sides.
To find the area and perimeter of polygons, we can use these formulas and plug in the given values. We can also use a ruler to measure the lengths of the sides and a protractor to measure the angles if they are not given.
-
Understanding circles, diameter, radius, and circumference in 5th Grade Geometry
A circle is a shape with no corners or sides. It has one curved edge equally distant from a fixed point called the center. A circle has some essential parts and properties that we need to know.
The diameter of a circle is the distance across it through the center. The radius of a circle is half of the diameter or the distance from the center to any point on the edge. The circumference of a circle is the length of its edge or boundary.
There is a special relationship between any circle's diameter and circumference. It is called pi (π), an irrational number approximately equal to 3.14 or 22/7. Pi is the ratio of the circumference to the diameter of any circle. In other words, dividing the circumference by the diameter means we get pi.
We can use pi to find the circumference or diameter of any circle if we know one of them. The formulas are:
- Circumference = pi times diameter
- Diameter = circumference divided by pi
We can also use pi to find the area of any circle if we know its radius or diameter. The formula is:
- Area = pi times radius squared
We can use these formulas to find the diameter, radius, circumference, or area of circles and plug in the given values. We can also use a ruler to measure the diameter or radius and a string to measure the circumference if they are not given.
-
Applying geometry to real-world problems
Geometry is not only about shapes and formulas. It is also about how we can use them to solve real-world problems. Geometry helps us understand the world around us and make sense of it.
For example, geometry can help us with the following:
- Design and build structures such as houses, bridges, towers, etc.
- Measure distances, angles, areas, perimeters, volumes, etc.
- Create maps, models, graphs, charts, etc.
- Navigate directions, locations, positions, etc.
- Draw and paint art, patterns, designs, etc.
- Play games, puzzles, sports, etc.
Geometry is everywhere; we can use it to explore and discover new things. Geometry also helps us develop our logical and creative thinking skills. By learning geometry, we can improve our problem-solving and reasoning abilities.
Bonus: Online resources to reinforce geometry math skills for 5th graders
If you want more resources to reinforce your 5th graders’ geometry math skills, here are some online resources that you can use:
- com: This website offers a variety of worksheets, games, guided lessons, and workbooks that cover 5th-grade geometry topics, such as classifying two-dimensional figures, finding volume and surface area, and using coordinate planes. You can browse the resources by skill or topic and download them for free. (https://www.education.com/resources/fifth-grade/geometry/)
- IXL: This website provides interactive math practice for 5th-grade geometry skills, such as multiplying and dividing by 2-digit numbers, estimating quotients, and using properties of multiplication and division.
You can track students’ progress, and they earn awards as they master each skill. You can also choose a skill plan that aligns with your textbook, state standards, or standardized test. (https://www.ixl.com/math/grade-5)
- Khan Academy: This website offers video lessons, exercises, quizzes, and articles that cover 5th-grade geometry topics, such as fractions and decimals, volume and unit conversion, graphing points, and interpreting data. Students can learn at their own pace and get feedback and hints as they practice. This course is aligned with Common Core standards. (https://www.khanacademy.org/math/cc-fifth-grade-math)
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
In this article, we have learned some basic concepts, questions, examples, and practice problems of 5th-grade geometry. We have also seen how geometry can be applied to real-world situations and how it can help us think logically and creatively.
Geometry is a fun and valuable subject that can enrich our lives and minds. By learning geometry, we can appreciate the beauty and order of natural shapes and patterns and human-made creations. We can also enhance our imagination and curiosity by creating shapes and designs.
We hope you enjoyed this article and learned something new. If you have any questions or comments, please share them below. Thank you for reading!