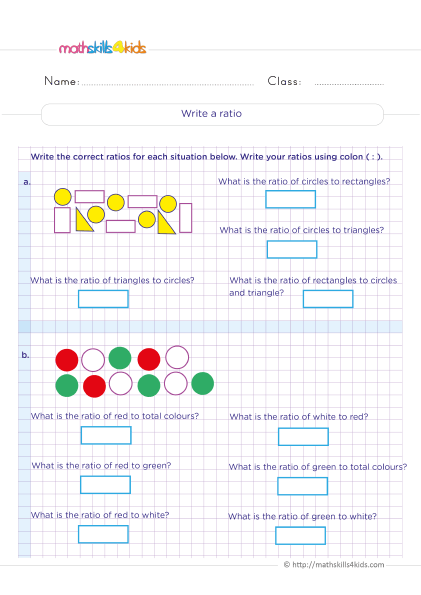
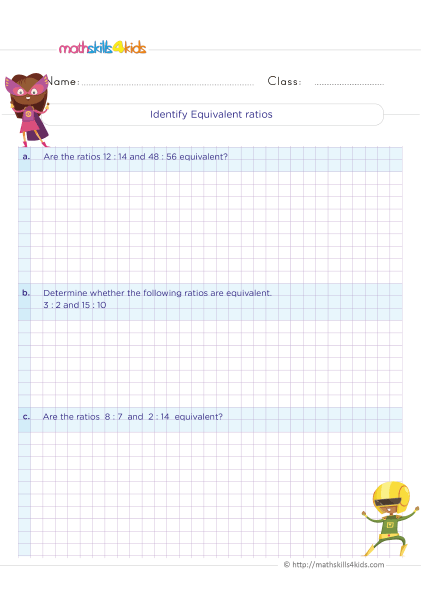
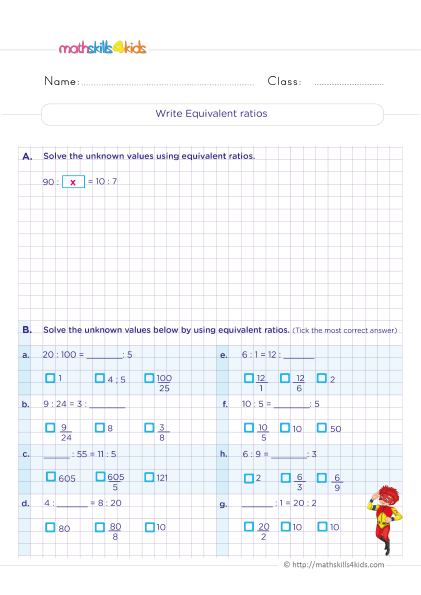
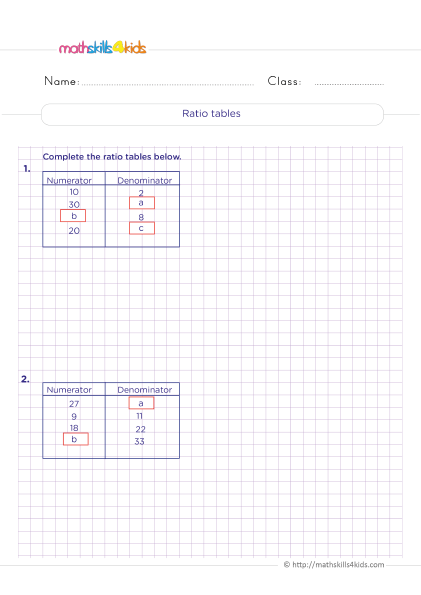
Grade 5 Math Worksheets: Ratio, Equivalent Ratios, and Rates

A ratio is a way of comparing two or more quantities of the same kind. For example, if you have 3 apples and 6 oranges in a basket, you can compare the number of apples to the number of oranges using a ratio. There are different ways of writing a ratio, such as:

• Using a colon (:), like 3:6
• Using the word "to," like 3 to 6
• Using a fraction (/), like 3/6

All these ways mean the same thing, i.e., for every 3 apples, there are 6 oranges in the basket. You can also write a ratio using different units as long as they measure the same kind of quantity. For example, you can write the ratio of 3 feet to 6 inches as:

• 3 feet: 6 inches
• 3 feet to 6 inches
• 3 feet / 6 inches

All these ways mean the same thing, i.e., for every 3 feet, there are 6 inches. However, it is usually easier to work with ratios that use the same units, so we can convert them if needed. For example, we can convert 3 feet to 36 inches and write the ratio as:

• 36 inches: 6 inches
• 36 inches to 6 inches
• 36 inches / 6 inches

All these ways mean the same thing, i.e., for every 36 inches, there are 6 inches.

Sometimes, we want to simplify a ratio to make it easier to understand or compare. To simplify a ratio, we divide both quantities by a common factor. A common factor is a number that can divide both quantities evenly without leaving any remainder. For example, if we want to simplify the ratio of 36 inches to 6 inches, we can divide both quantities by 6, which is a common factor. We get:

• (36 / 6) inches : (6 / 6) inches
• (36 / 6) inches to (6 / 6) inches
• (36 / 6) inches / (6 / 6) inches

Simplifying these expressions, we get:

• 6 inches: 1 inch
• 6 inches to 1 inch
• 6 inches / 1 inch

All these ways mean the same thing: for every 6 inches, there is 1 inch. This is the simplest ratio form because we cannot divide both quantities by any other common factor.

To compare two ratios, we can use cross-multiplication. Cross-multiplication determines which fraction is larger by multiplying the numerator (top number) of one fraction by the denominator (bottom number) of another fraction and vice versa. Then we compare the products (results of multiplication). For example, if we want to compare the ratios of 3:4 and 5:8, we can write them as fractions and cross-multiply:

• (3 / 4) vs (5 /8)
• (3 x 8) vs (4 x5)
• (24) vs (20)

Since 24 is larger than 20, we can say that (3 /4) is larger than (5 /8) or that (3:4) is larger than (5:8).

A rate is an exceptional ratio that compares two quantities of different kinds. For example, if you drive at a speed of 60 miles per hour, you are comparing the distance you travel (miles) to the time it takes you (hours). This is a rate. Rates are usually written using a fraction (/), like:

• Speed = distance/time
• Speed = miles/hour

To find a rate, we need to know two things: how much of one quantity there is and how much of another quantity there is. Then we divide one quantity by another quantity. For example, if you travel 120 miles in two hours, you can find your speed by dividing the distance by the time:

• Speed = distance/time
• Speed = miles/hour
• Speed =120 miles /2 hours
• Speed =60 miles per hour

This means that for every hour you drive, you travel 60 miles.

Sometimes, we want to convert a ratio to a rate or a rate to a ratio. To do this, we will use the same units for both quantities and multiply or divide by a conversion factor. A conversion factor is a fraction that equals 1 but has different units in the numerator and denominator. For example, if we want to convert the ratio of 3 feet to 6 inches to a rate of feet per inch, we can use the conversion factor of 12 inches per foot, which equals 1:

• 3 feet: 6 inches
• (3 feet x 12 inches / foot) / (6 inches x 1)
• (36 inches) / (6 inches)
• 6 inches/inch

This means that for every inch, there are 6 inches of length.

To convert a rate to a ratio, we can do the opposite: divide by a conversion factor. For example, if we want to convert the rate of 60 miles per hour to a ratio of miles to minutes, we can use the conversion factor of 60 minutes per hour, which equals 1:

• 60 miles/hour
• (60 miles x 1) / (1 hour x 60 minutes / hour)
• (60 miles) / (60 minutes)
• 1 mile/minute

This means that for every minute, there is 1 mile of distance.

Equivalent ratios are ratios that have the same value but use different numbers. For example, the ratios of 2:4 and 4:8 are equivalent because they both mean the same thing: for every 2 units of one quantity, there are 4 units of another quantity.

To find equivalent ratios, we can multiply or divide both quantities by the same number. For example, if we want to find an equivalent ratio for 2:4, we can multiply both quantities by 2:

• (2 x 2) : (4 x 2)
• 4:8

This is an equivalent ratio of 2:4. We can also divide both quantities by the same number. For example, if we want to find an equivalent ratio for 4:8, we can divide both quantities by 2:

• (4 /2) : (8 /2)
• 2:

This is an equivalent ratio of 4:8.

To demonstrate how equivalent ratios work, let's look at an example. Suppose you have a recipe for mixing 2 cups of flour with 4 cups of water to make a batter. How much flour and water do you need to make half as much batter?

To answer this question, we will find an equivalent ratio for the flour and water that is half as big as the original ratio. To do this, we can divide both quantities by 2:

• (2 cups /2) : (4 cups /2)
• 1 cup:2 cups

This means that if you want to make half as much batter, you will mix 1 cup of flour with 2 cups of water. This is an equivalent ratio to the original ratio of flour and water.

Now that we have learned what ratios, equivalent ratios, and rates are and how to work with them, let's have some fun and challenging activities to practice our skills! Here are some ideas:

• Make your recipe using ratios and rates. For example, you can make lemonade by mixing lemon juice, water, and sugar in a specific ratio. Please write your recipe using ratios and rates, then try it out. How does it taste? Can you adjust the ratio or rate to make it taste better?
• Find some real-life examples of ratios and rates around you. For example, you can look at the nutrition facts on food labels and find the ratios and rates of calories, fat, protein, sugar, etc., per serving. You can also look at the prices of different items and find the cost rates per unit. Write down some examples and compare them with your friends or family.
• Play some online games that involve ratios and rates. For example, you can play Ratio Blaster at https://www.mathplayground.com/ratioblaster.html, where you have to shoot at spaceships with matching ratios.

You can also play Ratio Martian at https://www.mathgames.com/skill/5.49-ratio-martian, where you have to help a Martian collect rocks with matching ratios. Have fun and challenge yourself!

Are you ready to test your 5h graders' skills on ratios and proportions? Here are 10 exercises that will challenge them to apply what they have learned. Don't worry; we will also show you how to solve them step by step. Let's get started!

1. A recipe for lemonade calls for 6 cups of water and 1 cup of lemon juice. How many cups of lemon juice are needed for 18 cups of water?

   Solution: To find the answer, we will use equivalent ratios. We can write the water-to-lemon juice ratio as 6:1 or 6/1. Then, we can set up a proportion with the unknown amount of lemon juice as x:

   6/1 = 18/x

   To solve for x, we cross-multiply:

   6x = 18

   Then, we divide both sides by 6:

   x = 18/6

   x = 3

   Therefore, we need 3 cups of lemon juice for 18 cups of water.

2. A map has a scale of 1 cm: 5 km. If two cities are 8 cm apart on the map, how far are they in real life?

   Solution: To find the answer, we will use rates. We can write the scale as a rate of 1 cm per 5 km or 1/5. Then, we can set up a proportion with the unknown distance as x:

   1/5 = 8/x

   To solve for x, we cross-multiply:

   x = 40

   Therefore, the two cities are 40 km apart in real life.

3. A bag contains 12 red marbles and 8 blue marbles. What is the ratio of red marbles to blue marbles? What is the ratio of blue marbles to total marbles?

   Solution: To find the answer, we will write the ratios in the simplest form. The ratio of red marbles to blue marbles is 12:8 or 12/8. To simplify this ratio, we divide both numbers by their greatest common factor, which is 4:

   12/8 = (12/4) / (8/4)

   12/8 = 3/2

   Therefore, the ratio of red marbles to blue marbles is 3:2.

   The ratio of blue marbles to total marbles is 8:20 or 8/20. To simplify this ratio, we divide both numbers by their greatest common factor, which is 4:

   8/20 = (8/4) / (20/4)

   8/20 = 2/5

   Therefore, the ratio of blue marbles to total marbles is 2:5.

4. A car travels at a speed of 60 miles per hour. How many miles does it travel in 15 minutes?

   Solution: To find the answer, we need to use rates. We can write the speed as a rate of 60 miles per hour or 60/1. Then, we can convert the time from minutes to hours by dividing by 60:

   15 minutes / 60 minutes = 0.25 hours

   Then, we can multiply the speed by the time to find the distance:

   60/1 x 0.25 = (60 x 0.25) / (1 x 1)

   60/1 x 0.25 = 15 / 1

   60/1 x 0.25 = 15

   Therefore, the car travels 15 miles in 15 minutes.

5. A recipe for lemonade calls for 6 cups of water and 2 cups of lemon juice. How many cups of lemon juice are needed for 18 cups of water?

   Solution: To solve this problem, we will find the water-to-lemon juice ratio in the recipe. We can write it as 6:2 or 6/2.

   Then, we will find an equivalent ratio with 18 as the first term. We can do this by multiplying both terms of the original ratio by 3 since 6 x 3 = 18.

   So, the equivalent ratio is 18:6 or 18/6. This means that for 18 cups of water, we need 6 cups of lemon juice.

6. A map has a scale of 1 cm: 5 km. How many centimeters on the map represent 20 km in reality?

   Solution: To solve this problem, we need to find the rate of centimeters to kilometers on the map. We can write it as 1 cm / 5 km.

   Then, we will find how many centimeters correspond to 20 km. We can do this by multiplying both terms of the original rate by 4 since 5 x 4 = 20.

   So, the equivalent rate is 4 cm / 20 km. This means that on the map, 4 centimeters represent 20 kilometers in reality.

7. A bag contains 12 red marbles and 8 blue marbles. What is the ratio of red marbles to blue marbles in simplest form?

   Solution: To simplify a ratio, we will find the greatest common factor (GCF) of both terms and divide them by it.

   The GCF of 12 and 8 is 4, so we divide both terms by 4 to get the simplest form. The simplified ratio is 12/4: 8/4 or 3:2.

   This means two blue marbles are in the bag for every three red marbles.

8. A car travels at a constant speed of 60 km/h for 2 hours. How far does it travel in total?

   Solution: To find the distance traveled by car, we need to multiply its speed by its time.

   The speed is given as a rate of kilometers per hour, and the time is given in hours. So, we multiply them to get the distance in kilometers.

   The distance is 60 km/h x 2 h = 120 km. This means that the car travels 120 kilometers in total.

9. A school has a student-teacher ratio of 25:1. How many students are in a class with four teachers?

   Solution: To find the number of students in a class, we will multiply the student-teacher ratio by the number of teachers.

   The ratio is a fraction of students per teacher, and the number of teachers is a whole number. So, we multiply them to get the number of students as a whole number.

   The number of students is (25/1) x 4 = 100. This means that there are 100 students in a class with four teachers.

10. A painting is enlarged by a scale factor of 1.5. If the original painting has a width of 40 cm and a height of 30 cm, what are the dimensions of the enlarged painting?

    Solution: To find the dimensions of an enlarged or reduced figure, we need to multiply the original dimensions by the scale factor.

    The scale factor is a decimal number representing how much bigger or smaller the figure becomes. So, we multiply both dimensions by 1.5 to get the new dimensions.

    The width of the enlarged painting is (40 cm) x (1.5) = (60 cm). The height of the enlarged painting is (30 cm) x (1.5) = (45 cm).

    This means that the enlarged painting has a width of 60 cm and a height of 45 cm.