Mastering 3D shapes with Grade 5 solid figures worksheets
Do you want to boost your 5th grader’s confidence in mastering 3D shapes? Then this article is for you. With Mathskills4kids’ Grade 5 solid figures worksheets practice, your students learn how to identify and classify three-dimensional shapes using their properties, draw and model three-dimensional shapes using nets and solids, and calculate the surface area and volume of three-dimensional shapes in no time.
-
Do you also wish for your students to learn how to apply this vital concept of 3D geometry to real-world problems? Stay engaged in this article and enjoy our fun strategies. But before then, let’s find out what three-dimensional shapes are and why they are important.
Enhance geometry learning with our Grade 5 three-dimensional worksheets for homeschooling and classroom use.
Hello math lovers! Today, we are excited to offer you this remarkable collection of Grade 5 three-dimensional worksheets for homeschooling and classroom use to enhance geometry learning skills in 5th graders.
Geometry is one of the most fascinating and practical branches of mathematics. It helps us understand the shapes and structures of the world around us and how to measure and manipulate them.
In grade 5, students are introduced to three-dimensional shapes, which have length, width, and height. These three-dimensional shapes are also called solids or polyhedral.
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
5th GRADE MATH TOPICS
- Number sense
- Addition and subtraction
- Multiplication
- Division
- Exponents
- Number theory
- Decimals
- Add & subtract decimals
- Multiply decimals
- Divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Mixed operations
- Problems solving
- Ratios and rates
- Percentages
- Money Math
- Number sequences
- Coordinate graph
- Variable expressions
- Data and Graphs
- Probability and statistics
- Telling time
- Unit of measurements
- 2D figures
- Triangles & quadrilaterals
- Symmetry & transformations
- 3D figures
- Geometric measurements
-
Buying is supporting us!
Buy Now...
-
-
What are three-dimensional shapes, and why are they important?
Three-dimensional shapes are shapes that have length, width, and height. They can be thought of as containers that can hold objects or liquids. Some examples of three-dimensional shapes are cubes, spheres, cones, cylinders, pyramids, prisms, and polyhedrons.
Three-dimensional shapes are important because they help us model and understand the physical world. For example, we can use cubes to build houses, spheres to represent planets, cones to make ice cream, cylinders to store water, pyramids to design monuments, prisms to refract light, and polyhedrons to create sculptures.
Three-dimensional shapes also help us develop spatial reasoning skills, perfect for solving problems in science, engineering, art, and everyday life.
-
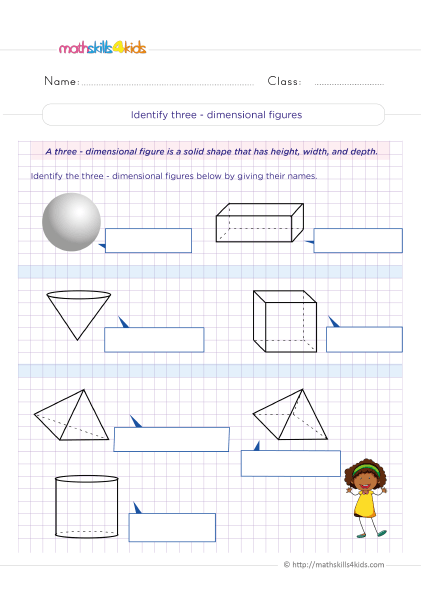
How to identify and classify three-dimensional shapes using their properties
One way to identify and classify three-dimensional shapes is by using their properties. Properties are characteristics or features that describe a shape. Some typical properties of three-dimensional shapes are:
- Faces: The flat surfaces that make up a shape. For example, a cube has six faces that are all squares.
- Edges: The line segments where two faces meet. For example, a cube has 12 edges equal in length.
- Vertices: The points where three or more edges meet. For example, a cube has eight vertices that are all right angles.
- Base: The face or faces a shape rests on or is built from. For example, a cone has one base that is a circle.
- Apex: The vertex or vertices opposite to the base or bases. For example, a cone has one apex that is a point.
- Cross-section: The shape formed when a plane cuts through a shape. For example, the cross-section of a cylinder can be a circle or an ellipse.
We can compare and contrast different three-dimensional shapes and group them into categories using these properties. For example, we can say that a cube and a rectangular prism belong to the same category because they both have six rectangular faces, 12 edges, and eight vertices.
However, they are different because a cube has all equal faces, edges, and angles, while a rectangular prism does not.
-
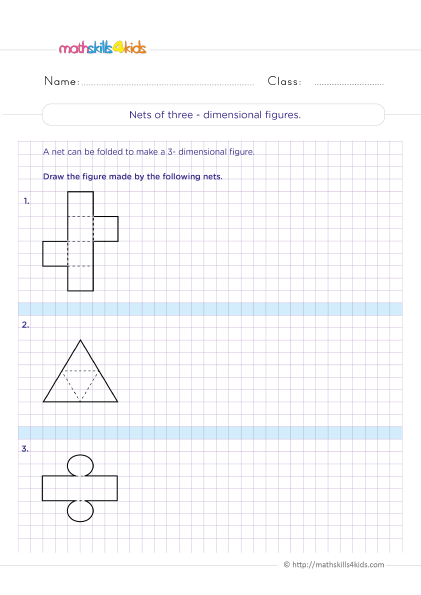
How to draw and model three-dimensional shapes using nets and solids
Another way to identify and classify three-dimensional shapes is using nets and solids. Nets are two-dimensional patterns that can be folded or cut out to form three-dimensional shapes. Solids are three-dimensional models made from materials like clay, paper, cardboard, or plastic.
Nets and solids help us visualize and represent three-dimensional shapes in different ways. For example, we can use nets to show how the faces of a shape are connected and arranged. We can also use solids to show the shape's appearance in real life.
To draw a net of a three-dimensional shape, we need to follow these steps:
- Identify the faces of the shape and their dimensions.
- Draw each face as a polygon on a flat surface.
- Connect the faces with tabs or flaps along their edges.
- Label the faces with letters or numbers for reference.
To make a solid from a net of a three-dimensional shape, we need to follow these steps:
- Cut out the net along its outline.
- Fold the net along its edges.
- Glue or tape the tabs or flaps together.
- Check if the solid matches the shape.
-
How to teach 3D shapes to 5th graders?
There are many ways to teach 3D shapes to 5th graders, but here are some of the most effective and fun ones:
- Use manipulatives: Manipulatives are physical objects that students can touch, move, and explore. They help students learn by doing and seeing. You can use various manipulatives to teach 3D shapes, such as wooden blocks, plastic models, clay, paper models, or even everyday items like cans, boxes, balls, etc.
You can ask students to identify the shapes, count their faces, edges, and vertices, compare their sizes and volumes, build new shapes from them, etc.
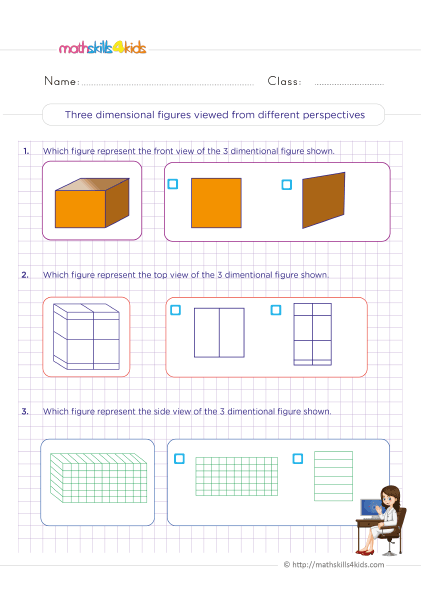
- Use drawings and diagrams: Drawings and diagrams are visual representations that help students understand the concepts and properties of 3D shapes. You can use drawings and diagrams to show students how to draw nets of 3D shapes, calculate their surface area and volume, identify their symmetries and cross-sections, etc.
You can also ask students to create drawings and diagrams of 3D shapes using rulers, compasses, protractors, etc.
- Use games and puzzles: Games and puzzles are interactive activities that make learning fun and challenging. They help students practice their skills and apply their knowledge in different situations. You can use games and puzzles to teach 3D shapes in various ways, such as:
- Matching games: Students have to match 3D shapes with their names or properties
- Sorting games: Students have to sort 3D shapes into different categories or groups based on their attributes
- Memory games: Students have to remember the location or features of 3D shapes on a grid or a board
- Tangram puzzles: Students have to use 2D shapes to form 3D shapes
- Jigsaw puzzles: Students have to assemble pieces of a net or a picture of a 3D shape
- Logic puzzles: Students have to use clues or rules to find out the missing information about a 3D shape
- Use manipulatives: Manipulatives are physical objects that students can touch, move, and explore. They help students learn by doing and seeing. You can use various manipulatives to teach 3D shapes, such as wooden blocks, plastic models, clay, paper models, or even everyday items like cans, boxes, balls, etc.
-
How to calculate the surface area and volume of three-dimensional shapes
Another vital skill students need to learn in grade 5 is calculating three-dimensional shapes' surface area and volume. The surface area is the total area of all the faces of a shape, and the volume is the amount of space that a shape occupies. These measurements can help us compare, design, and build different objects using three-dimensional shapes.
To calculate the surface area and volume of three-dimensional shapes, we need to use some formulas that depend on the shape and its dimensions. For example;
- The surface area of a cube is 6s2, where s is the length of a side, and the volume of a cube is s3.
- The surface area of a rectangular prism is 2(lw + lh + wh), where l, w, and h are the prism's length, width, and height, and the volume of a rectangular prism is lwh.
- The surface area of a sphere is 4πr2, where r is the radius of the sphere, and the volume of a sphere is (4/3)πr3.
To find the surface area and volume of more complex shapes, such as pyramids, cones, and cylinders, we can use strategies such as decomposing them into simpler shapes, using nets or formulas involving other measurements such as the base area or the slant height. For example;
- The surface area of a pyramid is B + (1/2)pl, where B is the base area, p is the perimeter of the base, and l is the slant height
- The volume of a pyramid is (1/3)Bh, where h is the pyramid's height.
-
How to apply the concepts of three-dimensional geometry to real-world problems
Learning how to work with three-dimensional shapes is fun and useful for solving real-world problems. For instance, we can design and build structures such as houses, bridges, towers, or sculptures using three-dimensional geometry.
We can also use three-dimensional geometry to measure and compare objects like boxes, cans, balls, or bottles. We can also use three-dimensional geometry to explore and understand natural phenomena such as crystals, planets, stars, or snowflakes.
Some examples of real-world problems that involve three-dimensional geometry are:
- How much paint do we need to cover a cube-shaped room with a side length of 10 feet?
- How many tennis balls can fit inside a cylindrical container with a radius of 6 inches and a height of 12 inches?
- What is the volume of cone-shaped ice cream with a radius of 2 inches and a height of 4 inches?
- How many faces does a dodecahedron have? How many vertices? How many edges?
- What is the shape of a snowflake? How can we draw it using a net?
Bonus: where to find additional resources to reinforce 5th graders’ 3D shapes skills
If you want to find more resources to help your 5th graders learn about 3D shapes, here are some websites that you can check out:
- Math is Fun (https://www.mathsisfun.com/geometry/solid-geometry.html): This website has a lot of information and examples about 3D shapes, as well as interactive quizzes and games.
- Khan Academy (https://www.khanacademy.org/math/basic-geo/basic-geo-volume-sa): This website has video lessons and exercises about the surface area and volume of 3D shapes.
- IXL (https://www.ixl.com/math/grade-5/properties-of-three-dimensional-figures): This website has practice questions and feedback about the properties of 3D shapes.
- Math Salamanders (https://www.math-salamanders.com/3d-geometric-shapes.html): This website has printable worksheets and nets of 3D shapes.
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
In this article, we have learned about three-dimensional shapes and how to enhance mastering 3D Shapes learning with our Grade 5 solid figures worksheets. We have learned how to identify and classify three-dimensional shapes using their properties, draw and model them using nets and solids, calculate their surface area and volume, and apply their concepts to real-world problems.
We hope that you have enjoyed this article and that you will try Grade 5 Mathskills4kids’ solid figures worksheets with your students or children. They are fun, engaging, and educative!