Tricks for learning multiplication tables | Times tables Memorisation techniques
The secret of understanding times table principles
Do you want to be a brain boxer in multiplication?
Hey this is the tricks for learning multiplication tables... in order to grab the secret of times tables Memorisation techniques, you just need some basic things:
- First, you can use the skip counting method, i.e counting in 2s, 3s, 4s, 5s, 6s, 7s, 10s etc.
- Secondly, you can use the number line method to make it easy.
Moreover, another secret which also is very simple is the repeated addition method, and of course the table method.
Hey now, let's discover tricks to use when multiplying basic numbers of 1 to 12, using some of our principles.
Tips for learning times tables
We shall begin with the zero (0) times table principle
Wow, very easy.
Any number multiplied by 0 gives 0.
Anytime you find a 0 in your multiplication question, then the answer to that question is automatically 0.
Example: 4 x 0 = 0; 0 x 8 = 0
The x1 principle is the best and easiest.
It actually do not require any technique.
Any number multiplied by 1 is simply that same number itself.
Example: 3 x 1= 3; 1 x 1= 1; 9 x 1= 9; 1 x 12= 12.
Do you know even numbers? Yes, then you've gotten it.
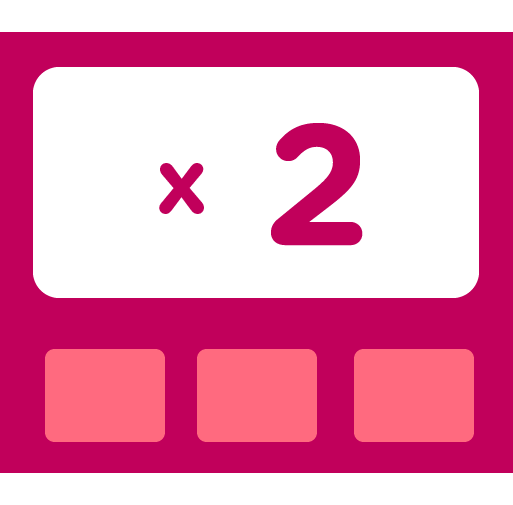
The best technique to apply in multiplication by 2 is just to skip count in 2s:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24.
Here you'll notice that your answers are all even numbers.
Example: 2 x 1 = 2; 2 x 2 = 4; 3 x 2 = 6; 2 x 4 = 8
Notwithstanding, another trick here could just be to ADD the number, which is supposed to be multiplied by 2, to that very number itself.
That means you should simply find the double of the number to multiply by 2.
Example: 2 x 3 = (3 + 3) = 6; 8 x 2 = (8 + 8) = 16; 5 x 2 = (5 + 5) = 10
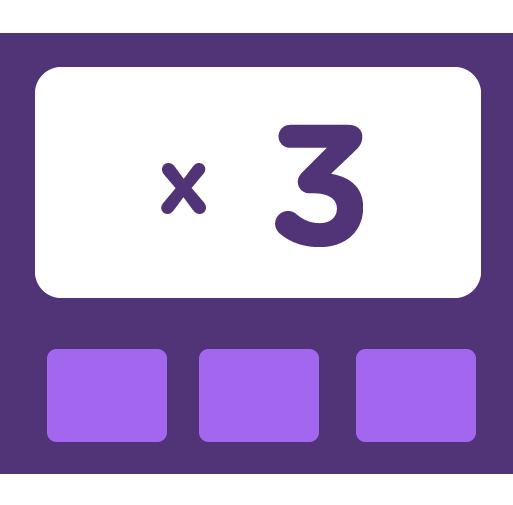
The fast and easiest way for a kid to know multiplication by 3 is simply to apply the skip counting method.
We will first of skip count in 3s.
Let's go: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36.
Now solve 3 x 4. Hey, it's easy.
Just go back to your skip counting line. Start counting from the 1st position which is 3, up to the 4th position.
You'll discover that the 4th position bears the number 12.
Hence, 3 x 4 = 12
However, another tip in the 3 times table is to multiply the given number by 2.
Then add the result to that same number, or you do the repeated addition method.
Example: 3 x 4 = (4 x 2) + 4 = 8 + 4 = 12 OR 4 + 4 + 4 = 8 + 4 = 12
Simple. Kids who are fast in addition can rely on this trick when multiplying number by 4.
This is because, multiplication by 4 is equivalent to multiplying that number by 2, two times.
When this is done, you however add the two results.
Example: 6 x 4= (6 x 2) + (6 x 2) 12 + 12 = 24
Multiplication by 5 is very easy to get familiar with.
At the start, you can even try skip counting aloud in 5s.
Let's try : 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60.
When you look keenly at the series of numbers above, you realise that each number ends with either a 5 or a 0.
Good. This means that an even number multiplied by 5 has a result that ends with 0, while an odd number multiplied by 5 has a result that ends with 5.
Example: 3 x 5 = 15; 6 x 5 = 30
This principle is very easy to grab.
We all know half of 6 is 3 right.
Ok. Given that you solve 8 x 6, the first thing to do is, simply multiply the given number (8) by 3;
do that exercise twice, however, obtaining two results.
Finally, you add the two results.
Example: 8 x 6= (8 x 3) + (8 x 3) = 24 + 24 = 48
Moreover, we never forget our skip counting method, which in 6s gives: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72.
As earlier stated, given 8 x 6 for example, simple count from the 1st position up to the 8th point.
You'll notice the 8th position is the number 48.
Having mastered your times table from 0 up to 6, you automatically have become an expert.
From x8 to x12 will therefore no longer be a problem, but will be easy to memorise.
Here, we simply use the skip counting method
Thus in 7s; 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 71, 84.
Given 7 x 8, as usual, begin counting from the 1st position which is 7, up to the 8th.
Having counted you realise that the 8th position bears the number 56. Hence, 7 x 8 = 56
So far, we've noticed that multiplication with an even number such as 4, 6, and 8 has a unique principle.
So, no stress here.
Now, that unique principle here is, using half of our even number for the exercise.
Now with the 8 times table, half of 8 is 4.
Perfect. Therefore given the problem 6 x 8, we simply multiply the given number (6) by 4.
As usual, the exercise is conducted twice.
Having obtained two results, you now add (two results).
Example: 6 x 8 = (6 x 4) + (6 x 4) = 24 + 24 = 48
Multiplication by 9 is one of the easiest times tables to remember.
Here it goes.
Given the problem 9 x 4, we can resolve it through these steps:
The first thing to do is to Add a 0 behind the number to be multiplied by 9.
If you do this your result will be 40.
Next, subtract that number (its value) from the gotten result (40 - 4) = 36.
9 x 4 = 36
Example:Example: 9 x 9 = 90 - 9 = 81; 7 x 9 = 70 - 7 = 63
Multiplication by tens is the best and simplest times table so far.
You don't need to think twice. Just add a 0 to the number you want to multiply with 10.
That's your answer.
You'll realise that your result has had an extra digit.
Example: 3 x 10 = 30 12 x 10 = 120
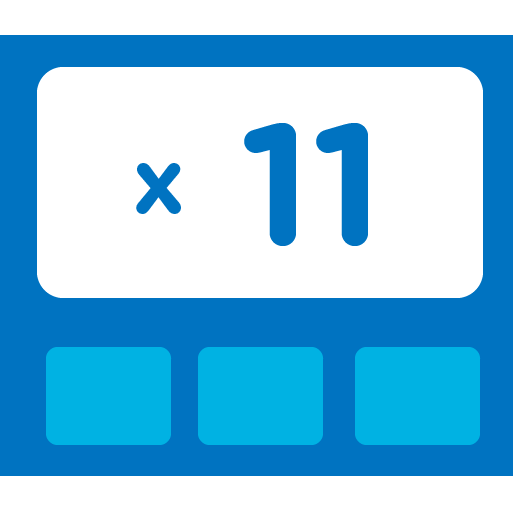
So far gone, you've noticed that any number multiplied by 11 means writing that number twice, or adding the same digit next to the present one.
Hey be careful! This rule applies only from 11 x 1 up to 11 x 9.
Example 1: 6 x 11= 66; 7 x 11 = 77;
For number 10, just add a 0 at the end of 11. So, 11 x 10 = 110
We have particular case here for numbers up to ten (11 x 11 and more). There is a simple formula to solve it. Let's try 11 x 12;
Example 2: 11 x 12 = (11 x 10) + (11 x 2) = 110 + 22 = 132
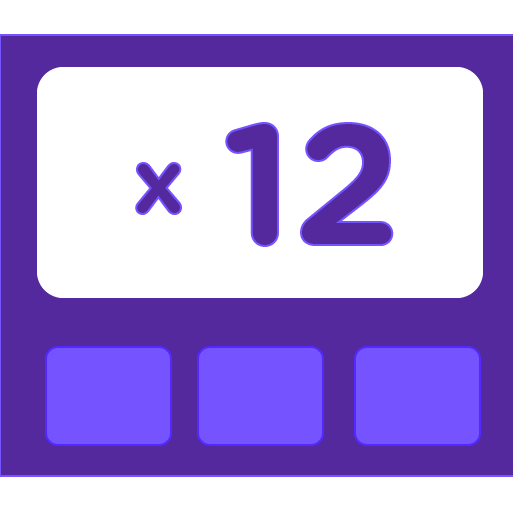
There's just a little practice quiz to be applied when multiplying a number by 12.
It's very easy. It goes thus: n x 12 = (n x 10) + (n x 2) [here n is a number]
Example: let's take n to be 3.
3 x 12 = (3 x 10) + (3 x 2) = 30 + 6 = 36
Therefore, 3 x 12 = 36
Yeeeeees, we've got it all. It's simple!






























 EXCELLENCE SKILLS ON TIMES TABLES EVALUATION
EXCELLENCE SKILLS ON TIMES TABLES EVALUATION