Free printable 2D shape activities for Grade 5: Learn geometry the fun way
Are you looking for some effective ways to help your 5th graders learn geometry the fun way? Do you want to offer them tips for quickly mastering 2-dimensional figures, especially polygons and circles? If so, you are in the right place! This article will provide free printable 2d shape activities for Grade 5 and the importance of learning this vital math concept.
-
In this article, we will explain the definitions of polygons and circles with examples, how to identify and classify polygons based on their sides and angles, and some common mistakes with 2D shapes recognition.
Most importantly, we’ll help your 5th graders learn how to compare and contrast polygons and circles using attributes and properties. We’ll also provide short questions helpful to review the main concepts. Above all, you will discover the best tips to make teaching 2-dimensional figures easy and fun for 5th graders.
In addition, we will share with you an amazing website, Mathskills4kids.com offering free printable worksheets and activities for learning geometry the fun way. Plus more resources that will help you find more enjoyable 2D shapes training activities for your 5th graders.
Let's get started!
Why learning 2D Shapes is essential for 5th Graders
Learning about 2-dimensional figures is an essential part of the Grade 5 math curriculum and a valuable skill for everyday life. By understanding the properties and relationships of 2D shapes, your 5th graders will be able to:
- Develop their spatial awareness and reasoning skills
- Enhance their creativity and imagination
- Solve problems involving geometry, measurement, and patterns
- Appreciate the beauty and diversity of shapes in nature and art
Also, learning about 2D shapes can prepare your 5th graders for more advanced topics in math, such as area, perimeter, volume, angles, symmetry, transformations, and coordinate geometry.
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
5th GRADE MATH TOPICS
- Number sense
- Addition and subtraction
- Multiplication
- Division
- Exponents
- Number theory
- Decimals
- Add & subtract decimals
- Multiply decimals
- Divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Mixed operations
- Problems solving
- Ratios and rates
- Percentages
- Money Math
- Number sequences
- Coordinate graph
- Variable expressions
- Data and Graphs
- Probability and statistics
- Telling time
- Unit of measurements
- 2D figures
- Triangles & quadrilaterals
- Symmetry & transformations
- 3D figures
- Geometric measurements
-
-
2D shapes -
Identifying a polygon practice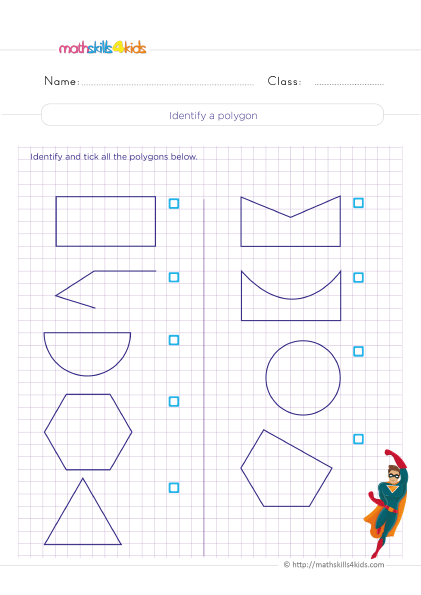 Print it...
Print it...
-
How to find the number of sides in a polygon
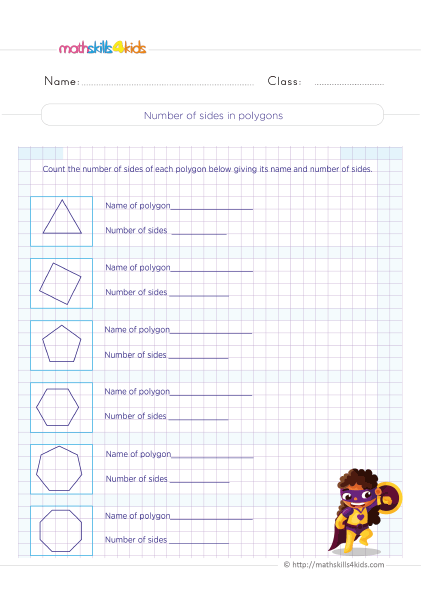 Print it...
Print it...
-
Lines, line segments, and rays
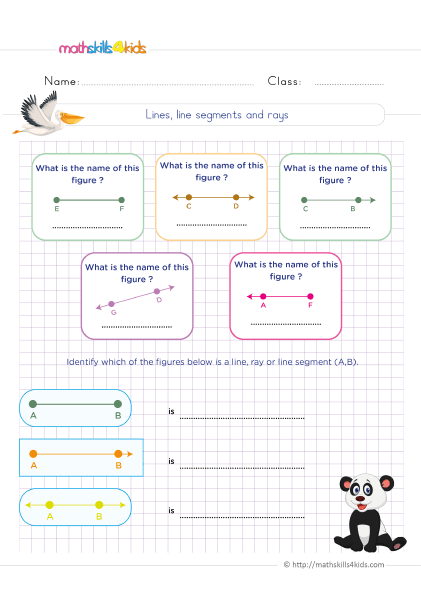 Print it...
Print it...
-
Parallel, perpendicular and intersecting lines practice
 Print it...
Print it...
-
Measure angles with a protractor independent practice
 Print it...
Print it...
-
Find missing angles in triangles and quadrilaterals
 Print it...
Print it...
-
2D shapes -
-
Buying is supporting us!
Buy Now...
-
-
What are polygons and circles? Definitions and Examples
Before we dive into the details of polygons and circles, let's review the definition of a 2-dimensional figure. A 2-dimensional figure is a shape that has length and width but no depth or thickness. It can be drawn on a flat surface like paper or a screen.
Some examples of 2-dimensional figures are squares, rectangles, triangles, circles, pentagons, hexagons, octagons, etc.
Among these 2 dimensional figures, polygons and circles are two essential categories your 5th graders need to know.
A polygon is a closed figure made up of straight-line segments that do not cross each other. The line segments are called sides, and the points where they meet are called vertices. The angle formed by two adjacent sides is called an interior angle.
Some examples of polygons are triangles, quadrilaterals (such as squares, rectangles, parallelograms, rhombuses, and trapezoids), pentagons, hexagons, octagons, etc.
A circle is a closed figure with points all the same distance from a fixed point called the center. The distance from the center to any point on the circle is called the radius. The length of the circle's boundary is called the circumference. The line segment that joins any two points on the circle and passes through the center is called the diameter.
Some examples of circles are coins, wheels, clocks, pizzas, etc.
-
How to identify and classify polygons based on their sides and angles
One of the vital skills that 5th graders need to master is identifying and classifying polygons based on their sides and angles. Polygons are closed shapes that are made of straight lines. The word polygon comes from the Greek words “poly,” meaning many, and “gon,” meaning angle. Therefore, a polygon is a shape with many angles.
There are different types of polygons, such as triangles, quadrilaterals, pentagons, hexagons, heptagons, octagons, nonagons, decagons, etc. The name of each polygon tells us how many sides it has. For example, a triangle has three sides; a quadrilateral has four sides; a pentagon has five sides, etc.
To identify and classify polygons, we need to look at two main features: the number of sides and the measure of the angles. As we saw above, the number of sides determines the polygon's name. The measure of the angles determines whether the polygon is regular or irregular.
A regular polygon is a polygon that has all sides equal and all angles equal. For example, a regular triangle (also called an equilateral triangle) has three equal sides and three equal angles of 60 degrees each. A regular quadrilateral (also called a square) has four equal sides and four equal angles of 90 degrees each.
An irregular polygon is a polygon that does not have all sides equal or all angles equal. For example, an irregular triangle (also called a scalene triangle) has three unequal sides and three unequal angles. An irregular quadrilateral (a trapezoid) has two pairs of parallel sides, but not all sides are equal.
To classify polygons based on their angles, we need to know the sum of the interior angles of a polygon. The interior angles are the angles inside the polygon. The sum of the interior angles depends on the number of sides of the polygon.
There is a simple formula to find the sum of the interior angles of any polygon:
The sum of interior angles = (n - 2) x 180 degrees, where n is the number of sides.
For example, to find the sum of the interior angles of a pentagon, we plug in n = 5 into the formula:
Sum of interior angles = (5 - 2) x 180 degrees
3 x 180 degrees
540 degrees
Therefore, the sum of the interior angles of a pentagon is 540 degrees.
Using this formula, we can classify polygons based on their angles into acute, right, and obtuse.
-
What is an acute polygon, a right polygon, and an obtuse polygon
An acute polygon is a polygon that has all interior angles less than 90 degrees. For example, a regular pentagon is an acute polygon because it has five interior angles of 108 degrees each, which are less than 90 degrees.
A right polygon is a polygon that has one or more interior angles equal to 90 degrees. For example, a square is a right polygon because it has four interior angles of 90 degrees each.
An obtuse polygon is a polygon that has one or more interior angles greater than 90 degrees. For example, an irregular hexagon can be an obtuse polygon if it has one or more interior angles greater than 90 degrees.
-
What are some common mistakes with 2d shapes recognition?
Below are some common mistakes most students make with 2 D shapes recognition:
- Confusing polygons with other shapes that are not polygons. For example, some students may think a circle is a polygon because it is round and closed. However, a circle is not a polygon because it does not have straight sides or corners. A circle is a different type of shape called a curve.
- Confusing regular polygons with other polygons that have similar names but are not regular. For example, some students may think that any four-sided shape is a square because they have heard the word square before.
However, not all four-sided shapes are squares. A square is a special type of four-sided shape with all sides and angles equal. Other four-sided shapes that are not squares include rectangles, parallelograms, rhombuses, trapezoids, and kites.
- Not paying attention to the attributes and properties of polygons when comparing and contrasting them. For example, some students may think that two polygons are the same if they look similar or have the same color or size. However, two polygons can look similar but have different attributes and properties.
For example, two triangles can look similar but have different side lengths or angle measures. To compare and contrast polygons accurately, students must look at their attributes and properties, such as the number of sides, angles, side lengths, angle measures, symmetry, and area.
-
How to compare and contrast polygons and circles using attributes and properties
One of the main goals of learning 2D shapes is to compare and contrast polygons and circles using their attributes and properties.
- Attributes are the features that describe a shape, such as color, size, or orientation.
- Properties are the rules that apply to a shape, such as formulas, relationships, or patterns.
To compare and contrast polygons and circles, we need to look at their attributes and properties and see how they are similar or different. For example, we can compare and contrast polygons and circles using the following attributes and properties:
- Number of sides: Polygons have a finite number of sides, while circles have an infinite number of sides.
- Number of angles: Polygons have a finite number of angles, while circles have no angles.
- Perimeter: Polygons have a perimeter that is the sum of the lengths of their sides, while circles have a perimeter called the circumference which is calculated by multiplying the diameter by pi (π).
- Area: Polygons have an area that is the amount of space inside them, while circles have an area that is calculated by multiplying the radius squared by pi (π).
- Symmetry: Polygons can have different types of symmetry, such as line symmetry, rotational symmetry, or point symmetry, while circles have infinite line symmetry and rotational symmetry.
- Tessellation: Polygons can tessellate or fit together without gaps or overlaps to cover a plane, while circles cannot tessellate.
-
Review the main concepts and give some tips for further practice
In this article, we have learned about polygons and circles, two types of 2D shapes that are important for 5th graders to master. We have learned how to identify and classify polygons based on their sides and angles, avoid some common mistakes with 2D shapes recognition, and compare and contrast polygons and circles using their attributes and properties.
To review the main concepts, here are some questions that you can ask yourself or your students:
- What is a polygon? What is a circle?
- How do you name a polygon based on its number of sides?
- How do you find the sum of the interior angles of a polygon?
- What is the difference between a regular polygon and an irregular polygon?
- What are the three categories of polygons based on their angles?
- What are some shapes that are not polygons? Why?
- What are some polygons that are not regular? Why?
- What attributes and properties can you use to compare and contrast polygons and circles?
To practice further, here are some tips that you can follow:
- Draw different types of polygons and circles on paper or using online tools. Label their sides, angles, perimeter, area, and symmetry. Try to draw both regular and irregular polygons.
- Use flashcards or games to memorize the names and features of different polygons and circles.
- Use worksheets or online quizzes to test your knowledge and skills on polygons and circles.
- Use real-life examples or models to explore polygons and circles in your surroundings. For example, you can use a pizza cutter to cut a pizza into different shapes and measure their angles or area.
Tips to make the teaching of 2-dimensional figures easy and fun for 5th Graders
Teaching 2-dimensional figures can be easy and fun for 5th graders using effective strategies and activities. Here are some tips that you can use to make the teaching of 2-dimensional figures engaging and enjoyable for your students:
- Use manipulatives or hands-on materials to help students visualize and explore 2-dimensional figures. For example, you can use geoboards, pattern blocks, tangrams, paper cut-outs, or origami to create different polygons and circles.
- Use songs or chants to help students remember the names and features of 2-dimensional figures. For example, you can use this song to teach students about polygons: https://www.youtube.com/watch?v=Q1xvpti6h0A.
- Use stories or comics to help students relate 2-dimensional figures to real-life situations or characters. For example, you can use this comic to teach students about the difference between regular and irregular polygons: https://www.mathsisfun.com/geometry/regular-polygons.html.
- Use games or puzzles to help students practice and reinforce their skills on 2-dimensional figures. For example, you can use this game to help students compare and contrast polygons and circles: https://www.mathplayground.com/shape_match.html.
- Use projects or challenges to help students apply their knowledge and creativity to 2-dimensional figures.
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
In conclusion, learning about 2D shapes is also essential for 5th graders and fun. Students can develop their spatial reasoning, problem-solving, and logical thinking skills by understanding the concepts of polygons and circles. They can also apply their knowledge to real-world situations and appreciate the beauty of geometry.
We hope this article has helped you learn how to form polygons and circles from scratch and how to compare and contrast them using attributes and properties. We also hope you have enjoyed some of the tips and resources we shared to make your teaching of 2-dimensional figures easy and fun for 5th graders.
