5th Grade symmetry and transformation worksheets: Free download
Are you a teacher or parent wishing to boost your student’s symmetry and transformation skills? Do you want to help them develop their spatial reasoning and geometric skills? If so, you've come to the right place! This article will provide us with a collection of fun 5th Grade symmetry and transformation worksheets from Mathskills4kids.com that are free to download and easy to print.
-
In this article, your 5th graders will learn how to transform objects, identify and draw lines of symmetry for different shapes, and how we can apply these vital concepts in real life.
Boost students’ math skills with these fun and engaging worksheets for learning about symmetry and transformation.
Hello! Get ready to boost your students’ math skills with these fun and engaging worksheets for learning about symmetry and transformation.
In this article, we will explore the importance of symmetry and transformation for 5th graders, what they are and how to teach them, and some examples and activities to make learning fun and engaging. We will also provide additional resources for teaching symmetry and transformation in Grade 5.
Let's get started!
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
5th GRADE MATH TOPICS
- Number sense
- Addition and subtraction
- Multiplication
- Division
- Exponents
- Number theory
- Decimals
- Add & subtract decimals
- Multiply decimals
- Divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Mixed operations
- Problems solving
- Ratios and rates
- Percentages
- Money Math
- Number sequences
- Coordinate graph
- Variable expressions
- Data and Graphs
- Probability and statistics
- Telling time
- Unit of measurements
- 2D figures
- Triangles & quadrilaterals
- Symmetry & transformations
- 3D figures
- Geometric measurements
-
Buying is supporting us!
Buy Now...
-
-
Importance of Symmetry and Transformation for 5th Graders
Symmetry and transformation are two crucial concepts in geometry that help us understand the properties and relationships of shapes. They also help us develop our spatial reasoning, which is the ability to visualize and manipulate shapes in our minds.
Spatial reasoning is a key skill for many fields of study and careers, such as engineering, architecture, art, design, science, and more. It also helps us solve everyday problems, such as reading maps, packing boxes, folding clothes, and playing games.
By learning symmetry and transformation, 5th graders can enhance their spatial reasoning and geometric skills, preparing them for more advanced math topics in middle school and beyond.
-
What are Symmetry and Transformation in Geometry?
In geometry, Symmetry and transformation are two ways of describing how shapes can change or stay the same. Symmetry is when a shape can be divided into two or more parts that are exactly the same. Transformation is when a shape can be moved, turned, flipped, or resized without changing its shape.
-
Overview of Mathskills4kids’ Grade 5 Symmetry and Transformation Worksheets
To help your 5th graders practice symmetry and transformation skills, we’ll have an overview of some worksheets created by Mathskills4kids.com, covering various topics and difficulty levels. These worksheets include:
- Identifying lines of symmetry for different shapes
- Drawing lines of symmetry for different shapes
- Performing and describing translations, rotations, reflections, and dilations of shapes
- Identifying congruent and similar shapes
- Finding missing angles and lengths of shapes using symmetry and transformation rules
- Applying symmetry and transformation concepts to real-world situations
You can download these worksheets for free from Mathskills4kids.com and print them out for your students. You can also find each worksheet's answer keys and explanations on this website.
-
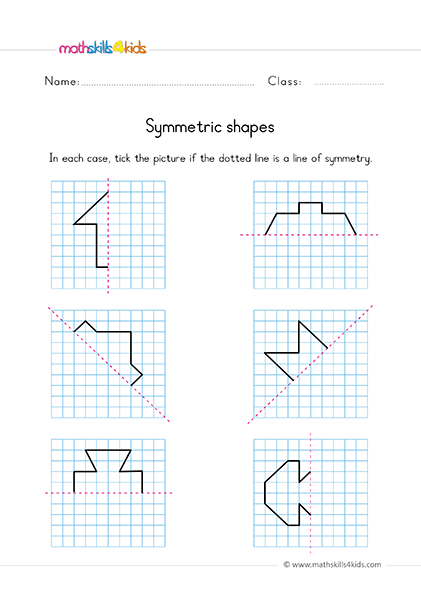
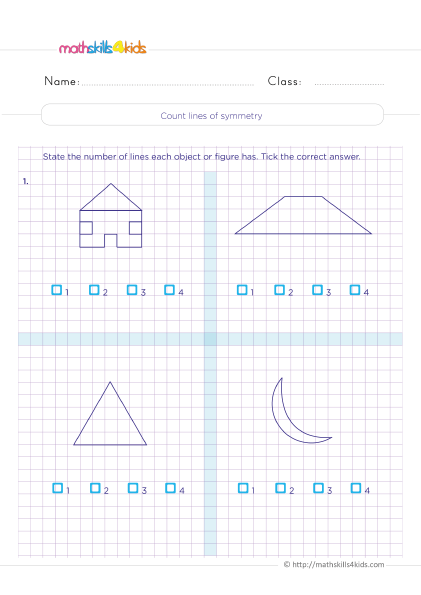
Symmetry: How to Identify and Draw Lines of Symmetry for Different Shapes
A line of symmetry is a line that divides a shape into two parts that are mirror images of each other. For example, a square has four lines of symmetry, one for each side. A circle has infinite lines of symmetry, because any diameter can divide it into two equal parts.
To identify lines of symmetry for different shapes, we can use a mirror or a paper fold test. We can place a mirror along the edge of a shape and see if the reflected part matches the original part. Or we can fold a paper cutout of a shape along a line and see if the two halves match.
To draw lines of symmetry for different shapes, we can use a ruler or a protractor. We can measure the length and angle of each side or vertex of a shape and draw a line that bisects them. Or we can use a compass or a circle template to draw circles or arcs that intersect at the center of a shape.
-
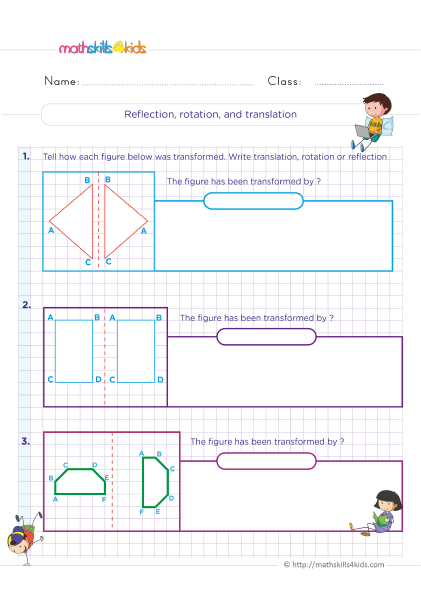
Transformation: How to Perform and Describe Translations, Rotations, Reflections, and Dilations of Shapes
A transformation is a change in a shape's position, orientation, or size. There are four types of transformations: translation, rotation, reflection, and dilation.
A translation is when a shape is moved from one place to another without changing its orientation or size. For example, sliding a triangle along a grid is a translation.
To perform a translation, we need to know the direction and distance of the movement.
To describe a translation, we can use words like "up," "down," "left," "right," or "diagonal," or we can use coordinates to show how much each point has moved.
A rotation is when a shape is turned around a fixed point without changing its size or shape. For example, spinning a square around its center is a rotation.
To perform a rotation, we need to know the center, angle, and direction of the turn.
To describe a rotation, we can use words like "clockwise" or "counterclockwise" or degrees to show how much the shape has rotated.
A reflection is when a shape is flipped over a line without changing its size or shape. For example, flipping a triangle over a horizontal line is a reflection.
To perform a reflection, we need to know the line of reflection.
To describe a reflection, we can use words like "horizontal," "vertical," or "diagonal," or we can use equations to show the slope and intercept of the line.
A dilation is when a shape is enlarged or reduced by a scale factor without changing its shape. For example, shrinking a circle by half is a dilation.
To perform a dilation, we need to know the center and the scale factor of the change.
To describe a dilation, we can use words like "enlarge" or "reduce," or we can use fractions or decimals to show how much the shape has changed in size.
-
Fun and engaging activities for teaching symmetry and transformation to 5th Graders
Besides worksheets, there are many other ways to make learning symmetry and transformation fun and engaging. Here are some fun and engaging activities for teaching symmetry and transformation to 5th Graders that you can do in the classroom or at home:
- Use mirrors, paper cutouts, tracing paper, or geoboards to explore lines of symmetry and transformations of shapes
- Use pattern blocks, tangrams, or origami to create symmetrical designs and figures
- Use grid paper, graph paper, or coordinate planes to draw and label translations, rotations, reflections, and dilations of shapes
- Use a protractor, a compass, or a ruler to measure the angles and lengths of shapes after transformations
- Use a camera, a computer, or a smartphone to take pictures of symmetrical objects or scenes in nature or the environment
- Use a kaleidoscope, a spinner, or a flip book to create symmetrical patterns or animations
-
Examples: How to apply symmetry and transformation concepts to real-world situations
Symmetry and transformation are useful in math and also in many real-world situations. Here are some examples of how we can apply symmetry and transformation concepts to everyday problems:
- Symmetry helps us design and create beautiful art, architecture, fashion, logos, flags, and more. It also helps us balance and organize objects or images.
- Transformation helps us move and manipulate objects or images in space. It also helps us create patterns, animations, games, puzzles, maps, and more.
- Congruence and similarity help us compare and measure objects or images with the same shape but different sizes or orientations. They also help us scale up or down objects or images without changing their shape.
- Angles and lengths help us calculate distances, directions, rotations, areas, perimeters, volumes, etc. They also help us construct shapes using tools or instruments.
Bonus: Additional resources for teaching symmetry and transformation in Grade 5
If you are looking for additional resources for teaching symmetry and transformation in Grade 5, here are some practical activities and resources that you can use in your classroom or at home:
- Symmetry and Transformation Worksheets: These printable worksheets provide practice problems and exercises on identifying and drawing lines of symmetry, performing and describing transformations, and applying symmetry and transformation concepts to real-world situations.
They are aligned with the Common Core State Standards for Grade 5 Geometry. You can download them for free from this link: https://www.mathworksheets4kids.com/transformation.php.
- Symmetry and Transformation Games: These online games are fun and interactive ways to reinforce the concepts of symmetry and transformation. They challenge students to use their spatial reasoning and problem-solving skills to complete various tasks involving shapes and patterns. You can find them on these websites: https://www.onlinemathlearning.com/transformation-games.html, https://www.matific.com/lk/en-gb/home/maths/grade-5/topics/geometry/symmetry-and-transformations/
- Symmetry and Transformation Videos: These videos are short and engaging explanations of the concepts of symmetry and transformation. They use animations, examples, and demonstrations to illustrate the definitions, properties, and applications of symmetry and transformation in geometry. You can watch them on these channels: https://www.youtube.com/watch?v=JX3VmDgiFnY, https://www.youtube.com/watch?v=XH8nSD4g0hg, https://www.youtube.com/watch?v=no9Drfcw2Zo.
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
Symmetry and transformation are essential topics in geometry that help students develop their spatial awareness, visual thinking, and logical reasoning skills. They also help students appreciate the beauty, order, and patterns in nature, art, architecture, and design.
Students can enhance their creativity, curiosity, and critical thinking abilities by learning about symmetry and transformation. They can also apply these concepts to other areas of math, such as algebra, fractions, measurement, and data analysis.
We hope this article has helped you understand the importance of symmetry and transformation for 5th graders. We also hope you have found valuable tips and resources for teaching these concepts to your students.
Remember that learning about symmetry and transformation can be fun and engaging using various methods, examples, and activities.