6th Grade 2D geometry worksheets: Shapes and their properties
-
Hello teachers and parents! Welcome to this outstanding 2D shapes math resource. In this article, you will discover the key to keeping your 6th graders engaged and excited about shapes and their properties. To make learning this vital math concept enjoyable and engaging, we will introduce you to Mathskills4kids.com, a fantastic website with a vast collection of 6th Grade 2D geometry worksheets designed to progressively build children’s math skills.
Explore the world of 2D geometry with our comprehensive resource for learning shapes and their properties.
Are you excited to explore the fascinating world of 2D geometry? This article is your ultimate guide to uncovering all the secrets! Get ready to be amazed by what you will discover.
With our comprehensive resource for learning shapes and their properties, 6th graders can identify common 2D shapes by their attributes, such as angles, sides, and symmetry.
Also, they learn how to draw them with simple tools and techniques.
Let's get started!
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
Buying is supporting us!
Buy Now...
-
-
What are 2D Shapes?
A 2D shape is a flat figure with only two dimensions: length and width. We can think of it as a shape that can be drawn on paper. Some examples of 2D shapes are circles, squares, triangles, and rectangles.
Can you name some more?
-
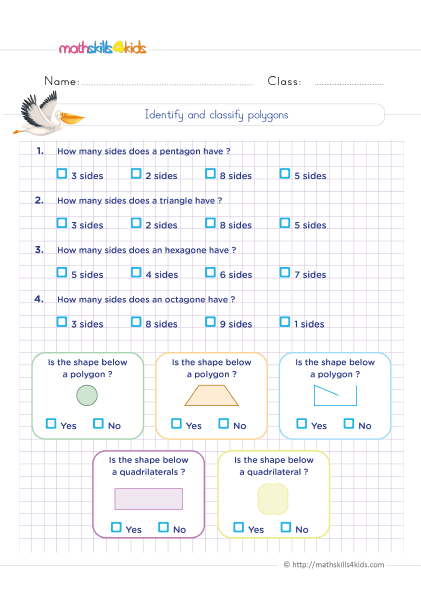
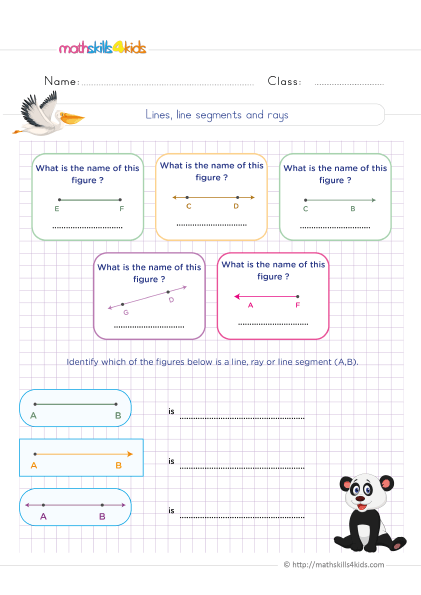
How to identify 2D shapes?
To identify 2D shapes, we can look at their features, such as the number of sides, the length of sides, the type of angles, and the number of lines of symmetry. For example, a square has four equal sides, four right angles, and four lines of symmetry. A circle has no sides, no angles, and infinite lines of symmetry.
What about a triangle? How many sides, angles, and lines of symmetry does it have?
-
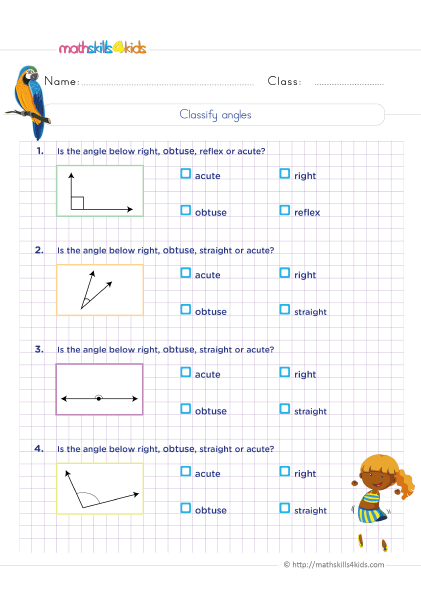
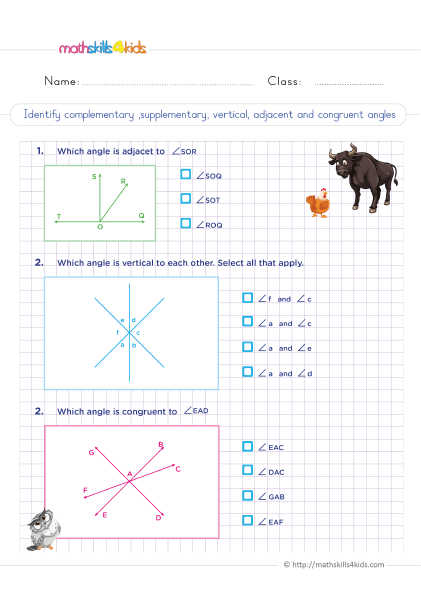
How to identify the different types of angles
An angle is the amount of turns between two lines that meet at a point. There are different types of angles, such as acute, right, obtuse, and straight angles.
- An acute angle is less than 90 degrees
- A right angle is exactly 90 degrees
- An obtuse angle is more than 90 degrees
- A straight angle is 180 degrees.
Can you find these angles in different shapes?
-
What are the different types of sides?
A side is a line segment that connects two vertices of a shape. A vertex is a point where two or more sides meet. There are different types of sides, such as equal, unequal, parallel, and perpendicular sides.
- Equal sides have the same length
- Unequal sides have different lengths
- Parallel sides never meet
- Perpendicular sides meet at right angles.
Can you spot these sides in different shapes?
-
What are types of symmetry?
Symmetry is when one part of a shape can be flipped, slid, or rotated to match another part. There are different types of symmetry, such as line, rotational, and point.
- Line symmetry is when a shape can be divided by a line into two identical parts.
- Rotational symmetry is when a shape can be rotated around a point and still look the same.
- Point symmetry is when a shape has a point the same distance from all its edges.
Can you find these symmetries in different shapes?
-
Common 2D Shapes and Their Properties
In this section of Mathskills4kids 6th Grade 2D Geometry worksheets, students will learn about some common 2D shapes and their properties, such as circles, squares, rectangles, triangles, pentagons, hexagons, octagons, and more.
They will also see examples of how these shapes are used in real life.
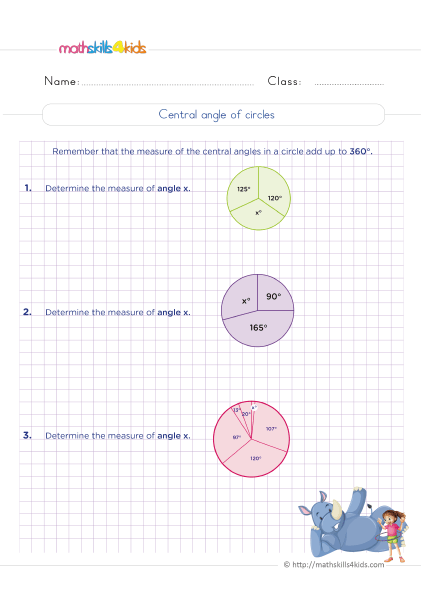
- Circle: A circle is a shape that has no sides or angles. It has one curved edge and one center point. The distance from the center to any point on the edge is called the radius. The distance across the circle through the center is called the diameter. The perimeter or circumference of a circle is the length of the edge. The area of a circle is the space inside it. We can find circles in many things, such as wheels, clocks, coins, and pizzas.
- Square: A square is a shape that has four equal sides and four right angles. It has four vertices and four lines of symmetry. The perimeter of a square is the sum of all its sides. The area of a square is the product of its side length and itself.
We can find squares in many things, such as tiles, windows, books, and chessboards.
- Rectangle: A rectangle is a shape that has four sides and four right angles. It has two pairs of equal and parallel sides. It has four vertices and two lines of symmetry. The perimeter of a rectangle is the sum of all its sides. The area of a rectangle is the product of its length and width.
We can find rectangles in many things, such as doors and screens.
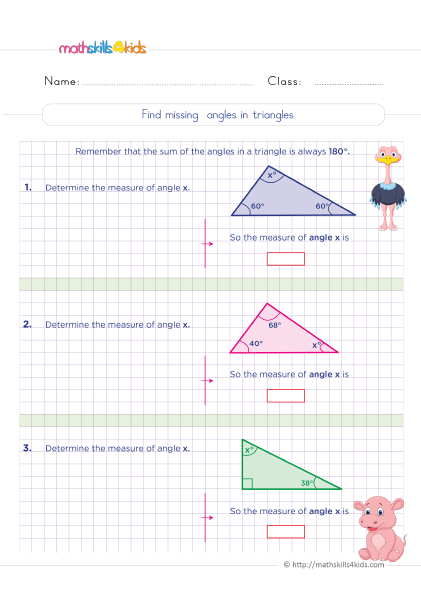
- Triangle: A triangle is a shape that has three sides and three angles. The sum of the angles in a triangle is 180 degrees. Different types of triangles are based on the length of their sides or the measure of their angles, such as equilateral, isosceles, scalene, acute, right, and obtuse. A triangle can have zero, one, or three lines of symmetry, depending on its type. A triangle can have rotational symmetry of order 1, 2, or 3, depending on its type.
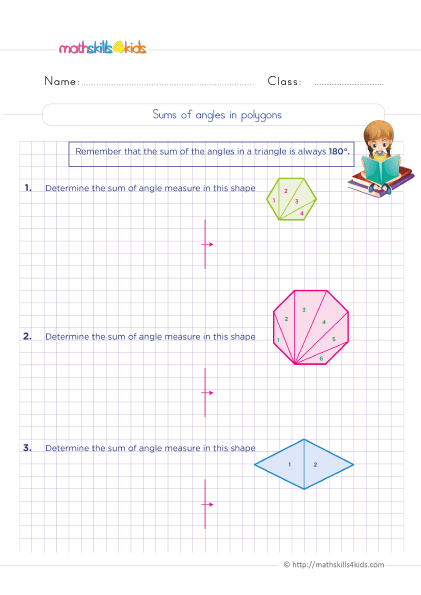
- Pentagon: A pentagon is a shape that has five sides and five angles. The sum of the angles in a pentagon is 540 degrees. There are different types of pentagons based on the length of their sides or the measure of their angles, such as regular, irregular, convex, and concave pentagons. A regular pentagon has five equal sides and five equal angles. It has five lines of symmetry and rotational symmetry of order 5.
- Hexagon: A hexagon is a shape that has six sides and six angles. The sum of the angles in a hexagon is 720 degrees. There are different types of hexagons based on the length of their sides or the measure of their angles, such as regular, irregular, convex, and concave hexagons. A regular hexagon has six equal sides and six equal angles. It has six lines of symmetry and rotational symmetry of order 6.
- Octagon: An octagon is a shape that has eight sides and eight angles. The sum of the angles in an octagon is 1080 degrees. There are different types of octagons based on the length of their sides or the measure of their angles, such as regular, irregular, convex, and concave octagons. A regular octagon has eight equal sides and eight equal angles. It has eight lines of symmetry and rotational symmetry of order 8.
-
How to Draw 2D Shapes
Drawing 2D shapes can be fun and easy if we follow simple steps and use helpful tools. Here are some tips and tricks to draw accurate and neat shapes.
- To draw a circle, use a compass or a circular object such as a coin or a lid. Place the point of the compass or the center of the object on the paper where you want to draw the circle. Then trace around the edge with a pencil or a pen.
- To draw a square, use a ruler or grid paper. First, draw a line segment with a desired length using the ruler or following the grid lines. Then use the ruler to measure 90 degrees from one endpoint and draw another line segment with the same length. Repeat this process until four connected line segments form a square.
- To draw a rectangle, use a ruler or grid paper. First, draw a line segment with a desired length using the ruler or following the grid lines. Then use the ruler to measure 90 degrees from one endpoint and draw another line segment with a desired width. Repeat this process until four connected line segments form a rectangle.
- To draw a triangle, use a ruler or a protractor. First, draw a line segment with a desired length using the ruler. Then use the protractor to measure a desired angle from one endpoint and draw another line segment with a desired length. Repeat this process until three connected line segments form a triangle.
- To draw a pentagon, use a ruler or a protractor. First, draw a line segment with a desired length using the ruler. Then use the protractor to measure 108 degrees from one endpoint and draw another line segment with the same length. Repeat this process until five connected line segments form a pentagon.
- To draw a hexagon, use a ruler or a protractor. First, draw a line segment with a desired length using the ruler. Then use the protractor to measure 120 degrees from one endpoint and draw another line segment with the same length. Repeat this process until six connected line segments form a hexagon.
- To draw an octagon, use a ruler or a protractor. First, draw a line segment with a desired length using the ruler. Then use the protractor to measure 135 degrees from one endpoint and draw another line segment with the same length. Repeat this process until eight connected line segments form an octagon.
Bonus: More engaging exercises to reinforce 6th grader's 2D geometry skill
If you want to give your 6th graders more practice to reinforce their 2D geometry skills, you can try online engaging exercises.
They are fun, interactive, and challenging.
- Shape Explorer: In this game, students can explore different 2D shapes and their properties, such as area, perimeter, angles, and symmetry. They can also create their own shapes and test their knowledge. https://www.mathsisfun.com/geometry/.
- Shape Patterns: In this game, students can complete different patterns using 2D shapes. They can also create their own patterns and challenge themselves. https://www.mathplayground.com/index_geometry.html.
- Shape Shoot: In this game, 6th graders can shoot down different 2D shapes based on their properties, such as the number of sides, number of angles, or type of symmetry. They can also choose different levels of difficulty and speed. https://www.mathsisfun.com/games/shape-shoot.html.
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
Congratulations, your 6th Grade students have learned a lot about 2D geometry! You have explored different shapes and their properties with them, such as angles, sides, and symmetry.
They have also learned to identify and draw 2D shapes using various tools and methods. They are now ready to apply their knowledge and skills to solve real-world problems involving 2D geometry.
Remember, geometry is fun and useful in many fields and situations.
Encourage your 6th graders to keep practicing and exploring the wonderful world of 2D geometry!