6th Grade adding and subtracting fractions: Free printable worksheets
Hello math teachers and parents! Do you have an impression that fractions are complicated to teach? If yes, check out Mathskills4kids’ 6th Grade adding and subtracting fractions free printable worksheets. In addition to Mathskills4kids.com, this article will provide more remarkable websites and resources that you can use to improve addition and subtraction of fractions skills in grade 6
-
Generally, our aim in this article is to provide fun and effective methods to help you teach fractions addition, and subtraction easier to your kids.
Nevertheless, we’ll briefly introduce why fraction math skills are important for 6th-Grade students. Then we’ll review some basic fractions concepts like fractions and how to compare, simplify and equivalent them.
In addition, we’ll provide step-by-step examples and practice problems for adding and subtracting fractions with like and unlike denominators. Also, we’ll illustrate some common Mistakes we make when adding and subtracting fractions and how to avoid them.
Fraction math skills for 6th Grade: Worksheets, Tips, and Tricks for Adding and Subtracting Fractions
Welcome to the world of fraction math skills for 6th grade! As students progress in their mathematical journey, fractions become essential to learning.
However, understanding and mastering this vital math concept can sometimes be challenging. That's where we come in! This article will provide you with various worksheets, tips, and tricks to help 6th graders excel in adding and subtracting fractions.
Whether you're a student looking for extra practice or a parent searching for resources to support your child's learning, this guide has got you covered. From step-by-step explanations to interactive exercises, we will break down the complexities of fractions into manageable pieces, making math fun and accessible.
So let's dive in and discover the secrets to mastering fraction math skills in 6th grade!
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
-
Adding and subtracting fractions with same denominator
 Print it...
Print it...
-
Add and subtract fractions with unlike denominators
 Print it...
Print it...
-
Adding and subtracting unlike fractions word problems
 Print it...
Print it...
-
Adding and subtracting mixed numbers
 Print it...
Print it...
-
Add and subtract mixed numbers word problems
 Print it...
Print it...
-
How to estimate sums and differences of mixed numbers
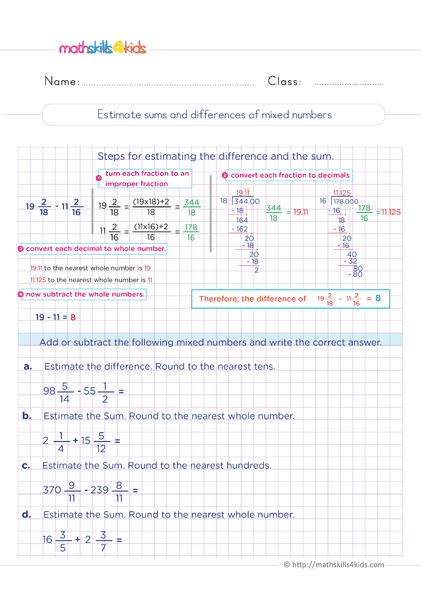 Print it...
Print it...
-
Adding and subtracting fractions with same denominator
-
Buying is supporting us!
Buy Now...
-
-
Why fraction math skills are important for 6th-Grade students
Fractions are everywhere in math and life. We use them to measure, compare, divide, and more. They are essential for understanding ratios, proportions, decimals, percentages, and algebra. That's why fraction math skills are important for 6th-grade students preparing for more advanced math topics in middle school and beyond.
But fractions can also be tricky and confusing. Many students need help with adding and subtracting fractions, especially when they have different denominators. They may make mistakes or get frustrated and give up. That's why we created this article to help 6th Grade students master fraction math skills for 6th grade so that by the end of this article, your 6th-graders will be able to solve fraction problems with confidence and accuracy.
-
Review of basic concepts: What are fractions, and how to compare, simplify, and equivalent them
Before diving into adding and subtracting fractions, let's review some basic concepts that 6th graders need to know. A fraction is a way of representing a part of a whole or a part of a group. A fraction has two parts: a numerator and a denominator. The numerator is the number above the fraction bar that tells us how many parts we have. The denominator is the number below the fraction bar that tells us how many parts the whole or the group is divided into.
For example, in the fraction 3/4, the numerator is 3, and the denominator is 4. This means we have 3 parts out of 4 equal parts of a whole or a group.
Comparing Fractions
One of the skills that students need to master when working with fractions is how to compare them. How do you know which fraction is larger or smaller than another? We can use two methods to compare fractions: cross-multiplying and finding a common denominator.
Cross-multiplying is a method that involves multiplying the numerator of one fraction by the denominator of another fraction and comparing the results. For example, to compare 2/3 and 3/5, we can cross-multiply as follows:
2/3 > 3/5
2 x 5 > 3 x 3
10 > 9
Since 10 is greater than 9, 2/3 is greater than 3/5.
Finding a common denominator is another method that involves making the denominators of two fractions the same by multiplying them by appropriate factors. For example, to compare 2/3 and 3/5, we can find a common denominator as follows:
2/3 > 3/5
2/3 x 5/5 > 3/5 x 3/3
10/15 > 9/15
Since both fractions have the same denominator, we can compare their numerators. Since 10 is greater than 9, 2/3 is greater than 3/5.
Simplifying Fractions
Another skill that you need to master when working with fractions is how to simplify them. Simplifying a fraction means reducing it to its lowest terms by dividing the numerator and the denominator by their greatest common factor (GCF). The GCF is the largest number that can divide both numbers evenly. For example, to simplify 12/18, we can find the GCF of 12 and 18 as follows:
12 = 2 x 2 x 3
18 = 2 x 3 x 3
GCF = 2 x 3 = 6
Then we can divide both the numerator and the denominator by the GCF as follows:
12/18 = (12 ÷ 6) / (18 ÷ 6)
12/18 = 2/3
The simplified fraction is 2/3.
Equivalent Fractions
A related skill important for 6th graders to master when working with fractions is how to equivalent them. Equivalent fractions have different numerators and denominators but represent the same value or amount. For example, 1/2 and 2/4 are equivalent fractions because they represent half of a whole or a group.
To find equivalent fractions, we multiply or divide the numerator and the denominator by the same number (except zero). For example, to find an equivalent fraction for 1/2, we can multiply both the numerator and the denominator by 2 as follows:
1/2 = (1 x 2) / (2 x 2)
1/2 = 2/4
The equivalent fraction is 2/4.
These are some basic concepts you need to know when working with fractions. Now let's practice adding and subtracting fractions with like and unlike denominators.
-
Adding fractions with like and unlike denominators: Step-by-step examples and practice problems for 6th Grade adding and subtracting fractions
As we said earlier, visit Mathskills4kids.com, where you’ll find a simple step-by-step guide with practice problems for 6th Grade adding and subtracting fractions.
Adding fractions is one of the operations we frequently encounter when working with fractions. To add fractions, we must follow different steps depending on whether the fractions have like or unlike denominators.
Like denominators are denominators that are the same. For example, 2/5 and 3/5 have like denominators because they have 5 as their denominator. Unlike denominators are denominators that are different. For example, 2/5 and 3/7 have unlike denominators because they have different numbers as their denominators.
To add fractions with like denominators, we need to follow these steps:
- Add the numerators and keep the denominator the same.
- Simplify the result if possible.
For example, to add 2/5 and 3/5, we can follow these steps:
2/5 + 3/5 = (2 + 3) / 5
2/5 + 3/5 = 5/5
2/5 + 3/5 = 1
The result is 1.
To add fractions with unlike denominators, we need to follow these steps:
- Find a common denominator by multiplying the denominators of both fractions.
- Multiply the numerator and the denominator of each fraction by the same factor to make them equivalent to the common denominator.
- Add the numerators and keep the denominator the same.
- Simplify the result if possible.
For example, to add 2/5 and 3/7, we can follow these steps:
2/5 + 3/7 = ?
Common denominator = 5 x 7 = 35
2/5 x 7/7 = 14/35
3/7 x 5/5 = 15/35
14/35 + 15/35 = (14 + 15) / 35
14/35 + 15/35 = 29/35
The result is 29/35.
Here are some practice problems for you to try adding fractions with like and unlike denominators. You can check your answers at the end of this post.
- Add: 4/9 + 2/9
- Add: 3/8 + 1/4
- Add: 5/12 + 7/18
- Add: 9/10 + 3/5
- Add: 7/15 + 4/15
-
Subtracting fractions with like and unlike denominators: Step-by-Step Examples and Practice Problems
Subtracting fractions is another operation that students will encounter frequently when working with fractions. To subtract fractions, we will follow similar steps as adding fractions depending on whether the fractions have like or unlike denominators.
To subtract fractions with like denominators, you need to follow these steps:
- Subtract the numerators and keep the denominator the same.
- Simplify the result if possible.
For example, to subtract 2/5 from 3/5, we can follow these steps:
3/5 - 2/5 = (3 - 2) / 5
So, 3/5 - 2/5 = 1/5
The result is 1/5.
To subtract fractions with unlike denominators, we need to follow these steps:
- Find a common denominator by multiplying the denominators of both fractions.
- Multiply the numerator and the denominator of each fraction by the same factor to make them equivalent to the common denominator.
- Subtract the numerators and keep the denominator the same.
- Simplify the result if possible.
For example, to subtract 2/5 from 3/7, we can follow these steps:
3/7 - 2/5 = ?
Common denominator = 5 x 7 = 35
2/5 x 7/7 = 14/35
3/7 x 5/5 = 15/35
15/35 - 14/35 = (15 - 14) / 35
15/35 - 14/35 = 1/35
The result is 1/35.
-
Common mistakes and how to avoid them: Tips and tricks for solving fraction problems accurately
One of the most challenging aspects of fraction math is avoiding common mistakes that can lead to incorrect answers. Here are some of the most frequent errors that 6th-grade students make when adding and subtracting fractions and how to avoid them.
- Forgetting to find the lowest common denominator (LCD) when adding or subtracting fractions with unlike denominators. The LCD is the smallest number that both denominators can divide into evenly. For example, the LCD of 3 and 4 is 12 because 12 is the smallest number that both 3 and 4 can divide into without a remainder.
To find the LCD, we can use prime factorization, which involves breaking down each number into its prime factors (the smallest numbers that can only be divided by themselves and 1). For example, the prime factors of 12 are 2, 2, and 3. Then, we multiply the highest power of each prime factor that appears in either denominator.
For example, the highest power of 2 in either 3 or 4 is 2, and the highest power of 3 in either 3 or 4 is 1. So, we multiply 2 x 2 x 3 to get 12, which is the LCD.
Once we find the LCD, we multiply each fraction by a factor that will make its denominator equal to the LCD. For example, to add 1/3 and 1/4, we multiply both fractions by a factor that will make their denominators equal to 12. We can do this by multiplying the numerator and denominator of each fraction by the same number.
For example, to make the denominator of 1/3 equal to 12, we need to multiply it by 4/4, which is equivalent to 1. This gives 4/12. Similarly, to make the denominator of 1/4 equal to 12, we need to multiply it by 3/3, which gives 3/12.
Now, we can add the fractions with like denominators: 4/12 + 3/12 = 7/12.
- Forgetting to simplify the final answer when adding or subtracting fractions. Simplifying means reducing the fraction to its lowest terms by dividing the numerator and denominator by their greatest common factor (GCF).
The GCF is the largest number that both numbers can divide into evenly. For example, the GCF of 8 and 12 is 4 because 4 is the largest number that both 8 and 12 can divide into without a remainder. To simplify a fraction, we divide the numerator and denominator by their GCF. For example, to simplify 8/12, we divide both numbers by their GCF of 4. This gives 2/3.
- Forgetting to change mixed numbers to improper fractions before adding or subtracting them. A mixed number is a number that consists of a whole number and a fraction, such as 2 1/2. An improper fraction is a fraction where the numerator is larger than or equal to the denominator, such as 5/2.
To add or subtract mixed numbers, we must first convert them to improper fractions. To do this, we multiply the whole number by the fraction's denominator and then add the numerator.
For example, to convert 2 1/2 to an improper fraction, multiply 2 by 2, then add 1. This gives 5. Then, write this number over the same denominator as the original fraction. This gives you 5/2.
- Forgetting to change improper fractions to mixed numbers after adding or subtracting them. Sometimes, after adding or subtracting fractions, we may end up with an improper fraction as the final answer. However, it is usually more convenient and easier to understand when converted back to a mixed number.
To do this, we divide the numerator by the denominator of the fraction and write the quotient as the whole number part of the mixed number. Then, we write the remainder over the same denominator as the original fraction.
For example, to convert 5/2 back to a mixed number, divide 5 by 2 and write 2 as the whole number part of the mixed number. Then, write 1 over 2 as the fractional part of the mixed number. This gives 2 1 / 2.
- Forgetting to find the lowest common denominator (LCD) when adding or subtracting fractions with unlike denominators. The LCD is the smallest number that both denominators can divide into evenly. For example, the LCD of 3 and 4 is 12 because 12 is the smallest number that both 3 and 4 can divide into without a remainder.
-
Tips and tricks for adding and subtracting fractions
Here are some tips and tricks to help your 6th graders master adding and subtracting fractions.
- Use visual aids such as fraction strips or circles to compare fractions with different denominators and see how they relate. For example, you can use fraction strips to help your students see that 1/2 equals 2/4, 3/6, 4/8, and so on.
You can also use fraction circles for them to see that 1/3 and 2/6 are equivalent because they cover the same amount of space in a circle divided into six equal parts.
- Encourage your students to use estimation to check their answers and see if they make sense. For example, if they add 1/4 and 2/3, they can estimate that the answer should be close to 1 because 1/4 is about a quarter of a whole, and 2/3 is about two-thirds of a whole. They may have made a mistake if they get an answer that is much larger or smaller than 1.
- Use mental math strategies to simplify fractions before adding or subtracting them. For example, if students add 2/6 and 3/9, ask them to simplify both fractions by dividing them by their GCF of 3. This gives them 2/6 = 1/3 and 3/9 = 1/3. Then, they can add the simplified fractions: 1/3 + 1/3 = 2/3.
- Use the butterfly method to add or subtract fractions with unlike denominators without finding the LCD. The butterfly method involves cross-multiplying the numerators and denominators of the fractions and then adding or subtracting the results. For example, to add 1 / 4 and 2 / 5 using the butterfly method, ask your students to cross-multiply 1 by 5, which gives 5, and 2 by 4, which gives you 8.
Then, let them add these numbers to get the answer's numerator: 5 + 8 = 13. Next, they’ll cross-multiply 4 by 5, which gives 20, and write this number as the answer's denominator: 13 / 20.
Finally, they’ll simplify the answer if possible: 13 / 20 cannot be simplified further, so it is the final answer.
- Use visual aids such as fraction strips or circles to compare fractions with different denominators and see how they relate. For example, you can use fraction strips to help your students see that 1/2 equals 2/4, 3/6, 4/8, and so on.
Bonus: Additional resources to improve 6th Grade addition and subtraction of fractions
If you want some additional resources for your kids to practice and improve their fraction math skills further, here are some 6th Grade addition and subtraction of fractions free printable worksheets, games, exercises, and quizzes that you can use:
- Online games and quizzes test your knowledge and speed of adding and subtracting fractions, such as https://www.mathsisfun.com/fractions_addition.html.
- Worksheets and exercises that provide step-by-step solutions and explanations for adding and subtracting fractions with like and unlike denominators, such as https://www.k5learning.com/free-math-worksheets/sixth-grade-6/fractions-addition-subtraction or https://www.math-drills.com/fractions.php.
- Videos and tutorials demonstrating how to add and subtract fractions using different methods and strategies, such as https://www.khanacademy.org/math/arithmetic/fraction-arithmetic.
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion: How to apply fraction math skills in real-life situations and beyond
Adding and subtracting fractions is vital for grade six math, many real-life situations, and beyond. Here are some examples of how to apply fraction math skills in everyday life:
- Cooking and baking: Many recipes use fractions to measure ingredients, such as cups, tablespoons, teaspoons, etc. We may need to add or subtract fractions to adjust the quantities or portions of the ingredients according to our needs or preferences.
- Shopping and budgeting: Many prices and discounts use fractions or percentages, such as half-price, 25% off, etc. We may need to add or subtract fractions to compare prices or calculate how much we’ve saved or spent.
- Sports and games: Many scores and statistics use fractions or decimals, such as batting averages, shooting percentages, etc. We may need to add or subtract fractions to compare different players' or teams' performances or outcomes.
- Art and music: Many patterns and rhythms use fractions or ratios, such as half-notes, quarter-notes, etc. We may need to add or subtract fractions to create or analyze different compositions or arrangements.
As you can see, fraction math skills are useful for many aspects of life. By learning to add and subtract fractions accurately and confidently in grade six, your students will be well-prepared for more advanced math topics in higher grades and beyond.
