6th Grade exponents and square roots worksheets: Free & Printable
Welcome to our comprehensive collection of free and printable 6th Grade Exponents and Square Roots Worksheets! Whether you're a student looking to sharpen your math skills or a teacher searching for valuable resources, you've come to the right place.
-
This article aims at helping 6th graders to understand exponents and square roots, why exponents and square roots are important in 6th-grade math, and the rules of exponents. In addition, we will provide some examples of simplifying expressions with exponents and finding square roots of perfect squares.
Furthermore, we will include diverse worksheets for practicing exponents and square roots that you can download and print from Mathskills4kids.com. Nevertheless, this article will illustrate examples of combining exponents and square roots in equations. You will also discover common mistakes to avoid when solving exponent and square root problems.
Finally, apart from Mathskills4kids.com, we will include additional resources for learning and practicing exponents and square roots.
Enjoy exponents and square roots: Conquer them with these free and printable worksheets for 6th Grade!
Hello parents and teachers! Help your students to enjoy exponents and square roots practice with these free and printable worksheets for 6th Grade designed to provide a fun and engaging learning experience.
From understanding the basic concepts of exponents to mastering the complexities of square roots, our worksheets cover a wide range of topics to ensure a well-rounded understanding of these fundamental mathematical principles.
Each worksheet is meticulously designed to combine educational value with interactive elements, making learning enjoyable and rewarding. So, get ready to unlock the mysteries of exponents and square roots, boost your math skills, and ace those tests with our free and printable 6th Grade Exponents and Square Roots Worksheets!
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
-
Writing multiplication expressions using exponents
 Print it...
Print it...
-
Find the missing exponent or base practice
 Print it...
Print it...
-
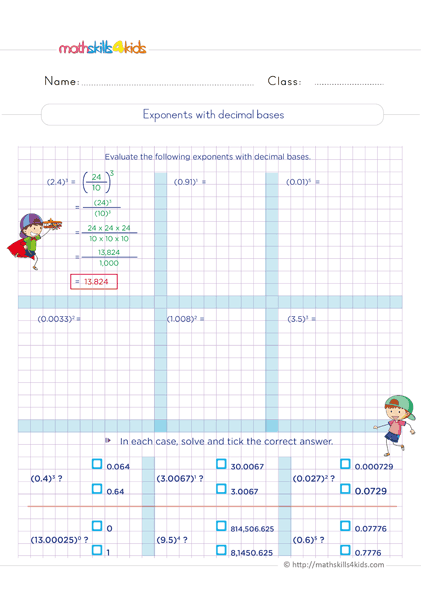
Exponeents with decimal bases
 Print it...
Print it...
-
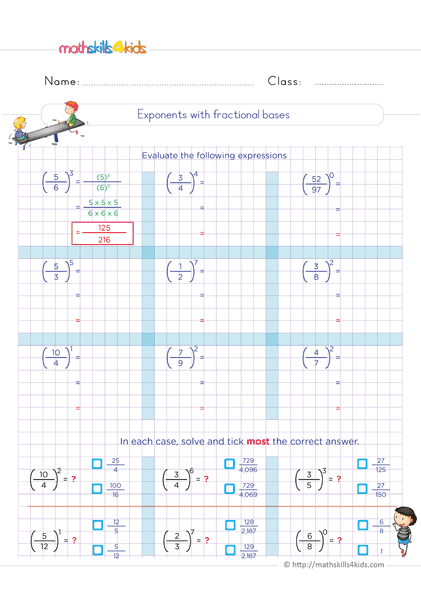
Exponenets with fractional bases
 Print it...
Print it...
-
Understanding negative exponents activity with answers
 Print it...
Print it...
-
Estimating square roots activity with answers
 Print it...
Print it...
-
Writing multiplication expressions using exponents
-
Buying is supporting us!
Buy Now...
-
-
Understanding exponents and square roots
Exponents and square roots are two ways of expressing repeated multiplication. For example, 23 means 2 multiplied by itself 3 times, which is 8. Similarly, the square root of 16 means the number multiplied by itself gives 16, which is 4. Exponents and square roots are also called powers and radicals, respectively.
-
Why are exponents and square roots important in 6th-grade math?
Exponents and square roots are important in 6th-grade math because they help students understand patterns, relationships, and properties of numbers. They also prepare them for more advanced topics in algebra, geometry, and science. For example, we can use exponents to represent very large or tiny numbers, such as the size of the universe or the mass of an atom.
Using the Pythagorean Theorem, we can also use square roots to find the length of the sides of a right triangle.
-
Rules of exponents
There are some rules that we must follow when working with exponents. These rules help us to simplify expressions and perform operations with exponents. Here are some of the most common rules of exponents:
- The product rule: Add the exponents when multiplying two powers with the same base. For example, 23 x 24 = 2(3+4) = 27.
- The quotient rule: Subtract the exponents when dividing two powers with the same base. For example, 25 / 22 = 2(5-2) = 23.
- The power rule: When raising a power to another power, multiply the exponents. For example, (23)4 = 2(3x4) = 212.
- The zero exponent rule: Any number raised to zero power equals one. For example, 20 = 1.
- The negative exponent rule: Any number raised to a negative power equals the reciprocal of that number raised to the positive power. For example, 2-3 = 1 / 23 = 1/8.
-
Simplifying expressions with exponents
To simplify expressions with exponents, we apply the rules of exponents and use the order of operations (PEMDAS). For example, to simplify the expression (23 x 4-2)2 / (8 x 2-1), we can follow these steps:
- Apply the power rule to the numerator and denominator: (26 x 4-4) / (8 x 2-1)
- Apply the product rule to the numerator and denominator: 2(6-4) x 4-4 / (8 x 2-1)
- Simplify the powers: 22 x (1/16) / (8 x (1/2))
- Multiply and divide from left to right: (4 x (1/16)) / (8 x (1/2))
- Cancel out common factors: (1/4) / (4/1)
- Invert and multiply: (1/4) x (1/4)
- Simplify the fraction: 1/16
-
Finding square roots of perfect squares
Another important skill for 6th-grade math is finding the square root of a number. The square root of a number is the number that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because 5 x 5 = 25.
A perfect square is a number that has a whole number as its square root. For example, 36 is a perfect square because the square root of 36 is 6, which is a whole number. Some other examples of perfect squares are 1, 4, 9, 16, and 49.
To find the square root of a perfect square, you can use a calculator or try to find the factors of the number that are equal. For example, to find the square root of 64, you can look for two factors of 64 that are the same: 8 x 8 = 64. So, the square root of 64 is 8.
-
Combining exponents and square roots in equations
Sometimes, you may encounter equations that involve both exponents and square roots. For example:
x2 = 49
To solve this equation, you need to find the value of x that makes the equation true. One way to do this is to take the square root of both sides of the equation. This will give you:
x = ±√49
The symbol ± means plus or minus. This means there are two possible x values: positive and negative. In this case, x can be either +7 or -7 because both numbers satisfy the equation.
x2 = 49
(+7)2 = 49
(-7)2 = 49
To check our answer, we can plug the values of x into the original equation and see if they make it true.
When solving equations with exponents and square roots, we must be careful with the signs and the order of operations. Remember to follow these rules:
- When taking the square root of both sides of an equation, include both the positive and negative solutions.
- When raising a negative number to an even power, use parentheses. For example, (-3)2 = 9, but -32 = -9.
- When raising a negative number to an odd power, we do not need parentheses. For example, (-3)3 = -27 and -33 = -27.
- When simplifying expressions with exponents and square roots, follow the order of operations: parentheses, exponents, multiplication/division, addition/subtraction (PEMDAS).
-
Printable worksheets for practicing 6equations with exponents and square roots
To help your 6th graders practice solving equations with exponents and square roots, we have prepared some more free and printable worksheets that you can download from Mathskills4kids.com and print at home or school. Each worksheet has an answer key for your convenience.
- Write multiplication expressions using exponents: This worksheet helps students practice writing repeated multiplication as powers. For example, 5 x 5 x 5 = 53.
- Evaluate powers: This worksheet helps students practice finding the value of power by multiplying the base by itself as many times as the exponent. For example, 24 = 2 x 2 x 2 x 2 = 16.
- Write powers of ten with exponents: This worksheet helps 6th graders practice writing powers of ten using exponents. For example, 10,000 = 104.
- Find the missing exponent or base: This worksheet helps students practice finding the missing exponent or base in a power equation. For example, 3? = 27 or ?2 = 49.
- Powers with decimal bases: This worksheet helps Grade 6 students practice finding the value of powers with decimal bases. For example, 0.13 = 0.001.
- Powers with fractional bases: This worksheet helps children practice finding the value of powers with fractional bases. For example, (1/2)3 = 1/8.
- Square roots of perfect squares: This worksheet helps learners practice finding the square root of a perfect square. A perfect square is a number that can be written as the product of two equal factors. For example, 64 is a perfect square because it can be written as 8 x 8 or (8)2. The square root of 64 is 8 because 8 x 8 = 64.
- Estimate square roots: This worksheet helps 6th graders practice estimating the square root of a non-perfect square by finding the two closest perfect squares and using them as a range. For example, to estimate the square root of 50, we can find that 49 and 64 are the closest perfect squares to 50. The square root of 49 is 7, and the square root of 64 is 8, so the square root of 50 is between 7 and 8.
Additional resources for learning and practicing exponents and square roots
If you need additional 6th Grade exponents and square roots worksheets for extra practice, we have some more resources for you here:
- [Exponents and Square Roots - Khan Academy](https://www.khanacademy.org/math/pre-algebra/pre-algebra-exponents-radicals): This online course covers the basics of exponents and square roots, including how to simplify expressions, compare numbers, and solve equations using these skills.
- [Exponents and Square Roots - Math Is Fun](https://www.mathsisfun.com/algebra/exponent-laws.html): This website explains the rules and properties of exponents and square roots, with examples and quizzes to test student’s understanding.
- [Exponents and Square Roots - IXL](https://www.ixl.com/math/grade-6/exponents-and-square-roots): This website offers online practice problems on exponents and square roots, with feedback and hints to help 6th graders improve their skills.
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
We hope you enjoyed this article about 6th Grade exponents and square roots. We also hope you found our free and printable worksheets valuable and fun.
Exponents and square roots are essential topics in math that will help 6th graders understand more advanced concepts in algebra, geometry, and calculus. They also have many applications in science, engineering, and everyday life.
If you want your students to practice more topics in math, or if you want to explore other grades and subjects, you can check out Mathskills4kids.com for more free and printable worksheets. We have worksheets for kindergarten to grade 12, covering topics such as arithmetic, fractions, decimals, percentages, ratios, proportions, algebra, geometry, trigonometry, statistics, probability, and more.
Thank you for reading this article, and happy teaching!
