6th Grade math dividing fractions worksheets: Free download
Does your 6th grader still find dividing fractions challenging? Not anymore. This article will share some fun, engaging 6th Grade math dividing fractions worksheets designed with educators and students in mind to provide a comprehensive learning experience. You can access a vast pack of these free downloadable dividing fractions worksheets from Mathskills4kids.com.
-
In this article, we’ll show you why dividing fractions is important in 6th-grade math and a perfect way to understand the concept of dividing fractions efficiently. Most importantly, we’ll pinpoint some common mistakes to avoid when dividing fractions. Plus, we’ll share additional resources for learning and practicing dividing fractions.
Let’s kick start!
How to master dividing fractions in 6th Grade Math: Engaging printable worksheets
Are you looking for a fun and effective way to help your 6th-grade students master the challenging concept of dividing fractions? Look no further! Our engaging printable worksheets are here to save the day. This article contains tips for mastering dividing fractions in 6th Grade Math.
With clear instructions and step-by-step examples, students will gain a solid understanding of dividing fractions in no time. Each worksheet is designed to keep students engaged and motivated, making math lessons exciting and enjoyable.
Thus, whether your students are visual, hands-on, or prefer a combination of both, our worksheets cater to various learning styles. So why wait? Help your students master dividing fractions with ease by downloading our 6th Grade math dividing fractions worksheets today for classroom and at-home practice.
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
Buying is supporting us!
Buy Now...
-
-
Why is dividing fractions important in 6th-grade math?
Dividing fractions is important in 6th-grade math for many reasons. First, aside from being an essential skill that students need to master in 6th grade, it helps them to understand the relationship between fractions, decimals, and percentages. It also helps them easily solve real-world problems involving ratios, proportions, and rates.
Dividing fractions helps students to:
- Understand the inverse relationship between multiplication and division. For example, if 3/4 x 4/5 = 12/20, then 12/20 ÷ 4/5 = 3/4.
- Simplify complex fractions. For example, if 2/3 ÷ 4/9 = x/y, then x/y is a simpler fraction than 2/3 ÷ 4/9.
- Convert fractions to decimals and percentages. For example, if 1/2 ÷ 1/4 = 2, then 1/2 = 0.5 and 1/4 = 0.25, so 0.5 ÷ 0.25 = 2.
- Solve real-world problems involving ratios, proportions, and rates. For example, if a recipe calls for 3/4 cup of flour for every 1/2 cup of sugar, how much flour do you need for 1 cup? The answer is 3/4 ÷ 1/2 = 3/2 or 1.5 cups of flour.
-
Understanding the concept of dividing fractions
Before we dive into step-by-step practice, let's ensure we understand what it means to divide fractions. When we divide two fractions, we ask how many times one fraction fits into another.
For example, if we want to divide 3/4 by 1/2, we ask how many halves are in three-fourths. This is similar to how we divide whole numbers, except that we work with parts of a whole instead of counting units.
-
Dividing fractions step-by-step
To divide two fractions, we need to follow these steps:
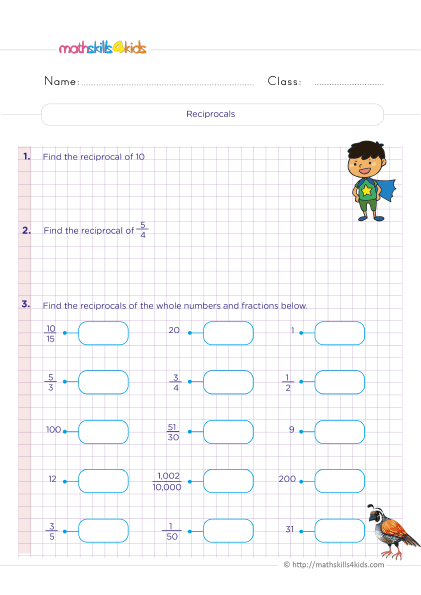
- Flip the second fraction upside down. This is called finding the reciprocal of the fraction. For example, the reciprocal of 1/2 is 2/1.
- Multiply the first fraction by the reciprocal of the second fraction. This is the same as multiplying the numerators and multiplying the denominators. For example, 3/4 x 2/1 = 6/4.
- Simplify the result if possible. This means finding the greatest common factor of the numerator and denominator and dividing both by it. For example, 6/4 can be simplified by dividing both by 2, which gives us 3/2.
That's it! We have successfully divided two fractions. Let's try another example: 5/6 ÷ 2/3.
- Flip the second fraction upside down. The reciprocal of 2/3 is 3/2.
- Multiply the first fraction by the reciprocal of the second fraction. 5/6 x 3/2 = 15/12.
- Simplify the result if possible. The greatest common factor of 15 and 12 is 3, so we can divide both by 3 to get 5/4.
-
Common mistakes to avoid when dividing fractions
When dividing fractions, there are some common mistakes to watch out for and avoid. Here are some of them:
- Forgetting to flip the second fraction upside down. This is a very common mistake that can lead to incorrect answers. Remember that we always need to find the reciprocal of the second fraction before multiplying.
- Flipping both fractions upside down. This is another common mistake that can also lead to incorrect answers. Remember that we need to flip only the second fraction, not the first one.
- Adding or subtracting instead of multiplying. Sometimes, students confuse dividing fractions with adding or subtracting fractions, which have different rules and procedures. Remember that when we divide fractions, we must multiply by the reciprocal, not add or subtract.
-
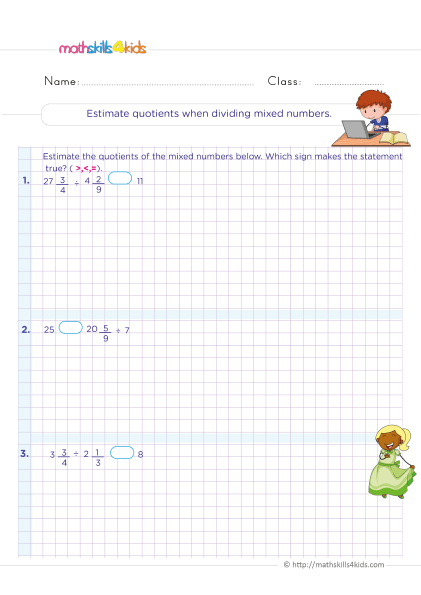
Engaging 6th Grade math dividing fractions worksheets practice
One of the best ways to master dividing fractions is to practice, practice, and practice! To help your 6th graders with that, we have selected some engaging 6th Grade math dividing fractions worksheets from Mathskills4kids.com that you can print, download and use for free.
These worksheets have different difficulty levels and include various problems involving dividing fractions by whole numbers, mixed numbers, and other fractions. They also have answer keys and explanations for each problem, so you can check students' work while they learn from their mistakes.
-
Tips for mastering dividing fractions in 6th-grade math
Dividing fractions may seem tricky initially, but with some tips and tricks, you can become a pro at it in no time. Here are some tips that we recommend for mastering dividing fractions in 6th-grade math:
- Use visual aids. Sometimes, it helps to use pictures or diagrams to understand what dividing fractions means and how it works. You can use fraction bars, number lines, area models, or other tools to help students visualize the problem and the solution.
- Use mnemonic devices. Mnemonic devices are memory aids that help students remember something by using a catchy phrase or acronym. For example, you can use the phrase "Keep Change Flip" to help learners remember the steps of dividing fractions: Keep the first fraction as it is, Change the division sign to a multiplication sign, and Flip the second fraction upside down.
- Practice with different types of problems. Don't limit your students to just one type of problem when practicing dividing fractions. Ensure that they solve problems that involve different types of fractions, such as proper fractions, improper fractions, mixed numbers, and decimals. This will help to develop their skills and confidence in dividing fractions.
Bonus: additional resources for learning and practicing dividing fractions
If you want your 6th graders to learn more about dividing fractions or practice more problems, here are some additional resources that we recommend:
- Khan Academy: Dividing fractions by fractions. This website has video lessons, interactive exercises, and quizzes to help 6th graders master dividing fractions by fractions. You can also track their progress and help them earn badges as they learn. https://www.khanacademy.org/math/arithmetic/fraction-arithmetic/arith-review-dividing-fractions/v/dividing-fractions.
- Math is Fun: Dividing Fractions. This website has clear explanations, examples, and diagrams to show students how to divide fractions. They can also try some online practice questions and see the answers with detailed solutions. https://www.mathsisfun.com/fractions_division.html.
- Math Playground: Fraction Games. This website has fun and engaging games that let students practice dividing fractions and other fraction skills. They can play against the computer or with a friend and choose from different difficulty levels. https://www.mathplayground.com/index_fractions.html.
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
Dividing fractions is an essential skill students master in 6th-grade math and beyond. It may seem challenging initially, but your 6th Grade math learners can easily conquer it with some understanding, practice, and tips.
We hope this article has helped you and your 6th Grade students learn more about dividing fractions and how to do it correctly and confidently.
Now that you have read this article, here are some next steps that you can take to help your students master dividing fractions:
- Download and print 6th Grade math dividing fractions worksheets from com and give your kids to solve them. Check their answers and explanations and show them where they made mistakes.
- Visit the websites we have recommended for you and explore the video lessons, exercises, games, and activities they offer. These websites will help your 6th graders to learn more about dividing fractions and provide more practice problems.
- Share this article with your friends, classmates, or family members who have kids in 6th Grade or are teaching dividing fractions. Help them learn more about this topic and improve their skills.
Thank you for reading this article, and we hope you enjoyed it. Happy learning, and good luck with dividing fractions!