6th Grade number theory worksheets: Free and Printable
If you are a 6th grader or tutor who wants to take 6th grader’s number sense skills to the next level, you are in for a treat. This article is your number-one resource with thrilling 6th Grade number theory worksheets designed to make learning engaging and enjoyable for your child. You can access a vast pack of these free and Printable number theory worksheets from Mathskills4kids.
-
Teaching Number Theory to 6th Graders: Worksheets, Activities, Tips, and Tricks
Are you ready to embark on a mathematical adventure with your 6th-grade students? Teaching number theory to 6th graders may seem daunting, but with the right resources and strategies, it can be an exciting and enriching experience for you and your students. In this comprehensive guide, we will explore a variety of worksheets, activities, tips, and tricks that will make learning number theory a breeze.
From prime numbers and multiples to divisibility rules and factorization, we will dive deep into the fascinating world of numbers. Our carefully curated worksheets will provide ample practice opportunities, while our engaging activities will encourage hands-on learning and critical thinking.
Whether you're a seasoned math teacher or a novice looking to spice up your lessons, this guide will equip you with the tools and knowledge to make number theory accessible and enjoyable for your 6th graders. So, let's get started on this mathematical journey together!
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
-
What are the prime and composite numbers from 1 to 100
 Print it...
Print it...
-
Understand how to write prime factorization with exponents
 Print it...
Print it...
-
How do you find the greatest common factor (GCF)
 Print it...
Print it...
-
Least common multiple (LCM) - How to find it
 Print it...
Print it...
-
How do you find the GCF and LCM in word problems
 Print it...
Print it...
-
Difference between whole numbers, rational numbers and integers
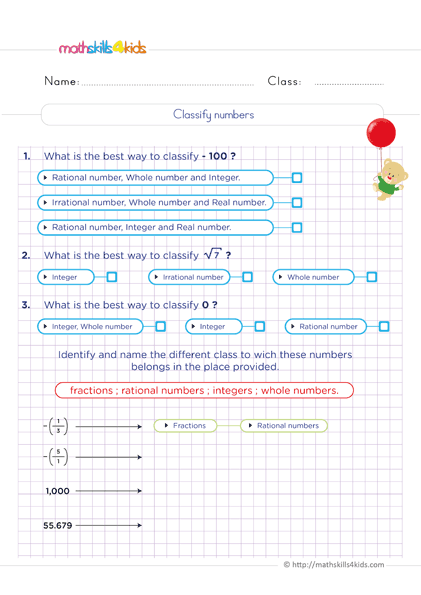 Print it...
Print it...
-
What are the prime and composite numbers from 1 to 100
-
Buying is supporting us!
Buy Now...
-
-
Why teach number theory to 6th graders?
Teaching number theory to 6th graders may seem abstract and advanced, but it has many applications and connections to other areas of mathematics and beyond. For example, number theory can help students understand divisibility, prime numbers, factors, multiples, remainders, modular arithmetic, cryptography, patterns, sequences, and more.
Number theory can also enhance students' logical thinking, problem-solving, creativity, and curiosity.
-
Benefits of teaching number theory at a young age
Teaching number theory to 6th graders can benefit their mathematical development and interest. Some of the benefits are:
- It can expose students to the beauty and diversity of mathematics and show them that math is about calculations, formulas, exploration, and discovery.
- It can challenge students to think critically and creatively and develop reasoning and proof skills.
- It can foster students' curiosity and enthusiasm for math and motivate them to learn more advanced topics.
- It can help students appreciate the connections between math and other disciplines, such as science, art, music, history, and cryptography.
- It can prepare students for higher-level math courses in middle and high school, such as algebra, geometry, calculus, and discrete math.
-
Number theory concepts suitable for 6th graders
Number theory is the branch of mathematics that deals with the properties and relationships of numbers, especially positive integers. Some number theory concepts suitable for 6th graders include divisibility, prime numbers, factors, multiples, remainders, modular arithmetic, and cryptography.
Some of these concepts may seem too advanced or abstract for 6th graders, but they can be introduced and explained in simple, concrete ways that make sense to young learners. For example, divisibility can be taught using examples of dividing candies or cookies among friends, prime numbers can be illustrated using patterns of dots or stars, factors and multiples can be related to multiplication tables and area models, remainders can be shown using pizza slices or chocolate bars, modular arithmetic can be demonstrated using clocks or calendars, and cryptography can be explored using secret codes or puzzles.
The key is to use familiar and relevant contexts, visual aids, manipulatives, and examples that help students connect number theory concepts to their prior knowledge and everyday experiences. By doing so, you can spark their curiosity and interest in learning more about the fascinating world of numbers.
-
Free and printable worksheets for teaching number theory
Worksheets are a helpful tool for teaching and practicing number theory concepts. They can provide students with structured, guided exercises reinforcing their understanding and skills. They can also help you assess their progress and identify their strengths and weaknesses.
Some of the crucial skills that 6th graders should learn in mathskills4kids’ free and printable 6th Grade number theory worksheets are:
- Identify factors: Factors are the numbers that can divide another number evenly. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Students should be able to find all the factors of a given number and identify if a number is prime or composite.
Prime numbers have only two factors: 1 and themselves. Composite numbers have more than two factors.
- Prime factorization: Prime factorization breaks down a composite number into its prime factors. For example, the prime factorization of 12 is 2 x 2 x 3 or 22 x 3. Students should be able to find the prime factorization of any composite number using factor trees or division methods.
- Prime factorization with exponents: Sometimes, it is more convenient to write the prime factorization of a number using exponents. For example, instead of 2 x 2 x 2 x 3 x 5, we can write 23 x 3 x 5. Students should be able to write the prime factorization of a number using exponents and convert from exponents to expanded form.
- Greatest common factor: The greatest common factor (GCF) of two or more numbers is the largest factor that they have in common. For example, the GCF of 12 and 18 is 6. Students should be able to find the GCF of two or more numbers using prime factorization or other methods.
- Least common multiple: The least common multiple (LCM) of two or more numbers is the smallest multiple that they have in common. For example, the LCM of 12 and 18 is 36. Students should be able to find the LCM of two or more numbers using prime factorization or other methods.
- GCF and LCM: word problems: Sometimes, we need to use GCF and LCM to solve real-world problems involving fractions, ratios, proportions, or divisibility. For example;
If we want to find how many cupcakes we can make with 12 eggs and 18 cups of flour, we need to find the GCF of 12 and 18, which is 6. Then, we can divide both numbers by 6 to get the ratio of eggs to flour, which is 2:3. I.e. for every 2 eggs, we need 3 cups of flour. Therefore, we can make 6 batches of cupcakes with these ingredients.
Students should be able to apply GCF and LCM to solve word problems like this.
- Sort factors of numerical expressions: A numerical expression combines numbers and operations, such as 2 + (3 x 4). A factor of a numerical expression is a number that can divide the expression evenly. For example, one factor of 2 + (9 x 2) is 2 because it can divide both terms evenly. Another factor is 10 because it can divide the whole expression evenly.
Students should be able to sort the factors of a numerical expression into two categories: factors that divide only one term evenly and factors that divide the whole expression evenly.
- Identify factors: Factors are the numbers that can divide another number evenly. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Students should be able to find all the factors of a given number and identify if a number is prime or composite.
-
Activities to make number theory fun and engaging
Worksheets are just one of many ways to teach number theory to 6th graders. You can also use activities that involve games, puzzles, challenges, experiments, projects, and more. These activities can make number theory fun and engaging for students by adding an element of playfulness, creativity, competition, collaboration, discovery, and application.
Some examples of activities that you can use to teach number theory to 6th graders are:
- Factor Bingo: This is a game where students have to find the factors of a given number and mark them on a bingo card. The first one to get a row, column, or diagonal of marked factors wins.
- Prime Number Sieve: This is an activity where students have to use a sieve (a grid of numbers) to cross out the multiples of 2, 3, 5, 7, etc. until they are left with only the prime numbers.
- Remainder Race: This is a game where students have to divide a given number by another number and find the remainder. The one who gets the smallest remainder wins.
- Clock Arithmetic: This is an activity where students have to use a clock (or a circular number line) to perform addition and subtraction operations modulo 12 (or any other number).
- Secret Code: This is an activity where students will use a simple cipher (such as Caesar cipher or substitution cipher) to encode and decode messages using modular arithmetic.
-
Tips for teaching number theory effectively
Teaching number theory to 6th graders can be challenging but rewarding. Here are some tips that can help you teach number theory effectively:
- Start with the basics: Before introducing any new concept or topic in number theory, ensure that your students have a solid foundation in the basic skills and concepts of arithmetic. Review the operations of addition, subtraction, multiplication, and division, as well as the properties of numbers, such as evenness, oddness, parity, and divisibility.
- Use multiple representations: To help your students understand and visualize number theory concepts, use multiple representations, such as words, symbols, diagrams, tables, charts, graphs, and models. For example;
You can use words to explain what a prime number is, symbols to write it in mathematical notation, diagrams to show it using dots or stars, tables to list some examples of prime numbers, charts to compare prime numbers with composite numbers, graphs to plot prime numbers on a number line, and models to demonstrate how prime numbers are used in cryptography.
- Connect to real-life situations: To make number theory relevant and meaningful for your students, connect it to real-life situations they can relate to and care about. For example, you can use examples of dividing candies or cookies among friends to teach divisibility, examples of secret codes or puzzles to teach cryptography, examples of clocks or calendars to teach modular arithmetic, and examples of encryption or decryption to teach applications of number theory.
- Encourage exploration and inquiry: To foster curiosity and interest in number theory, encourage your students to explore and inquire about the concepts and topics they are learning. For example, you can ask them to generate their questions, hypotheses, conjectures, and proofs about number theory, such as why there are infinitely many prime numbers, how to find the next prime number, what is the largest known prime number, and how to prove that a number is prime or composite.
You can also challenge them to find patterns, relationships, and generalizations among numbers, such as the Fibonacci sequence, the Sieve of Eratosthenes, the Goldbach conjecture, and the Riemann hypothesis.
- Provide feedback and support: To help your students succeed and improve in learning number theory, provide timely and constructive feedback and support. For example, you can praise their efforts and achievements, correct their errors and misconceptions, clarify their doubts and confusions, guide their thinking and problem-solving processes, and scaffold their learning and skill development.
-
Tricks to help students understand and apply number theory concepts
Number theory can be tricky and complex for some students. Here are some tricks that can help them understand and apply number theory concepts:
- Use mnemonics: Mnemonics are memory aids that help students remember information or rules. For example, you can use the acronym DUCKS to help students remember the divisibility rules for 2, 3, 4, 5, and 6. DUCKS stands for:
- D: Divisible by 2 if the last digit is even (0, 2, 4, 6, or 8).
- U: Divisible by 3 if the sum of the digits is divisible by 3.
- C: Divisible by 4 if the last two digits are divisible by 4.
- K: Divisible by 5 if the last digit is 0 or 5.
- S: Divisible by 6 if it is divisible by 2 and 3.
- Use shortcuts: Shortcuts are quick and easy ways to perform calculations or operations. For example, you can use the following shortcuts to find the factors or multiples of a number:
- To find the factors of a number, start with 1 and the number itself, then look for pairs of numbers that multiply to give the number. For example, to find the factors of 24, start with 1 and 24, then look for pairs of numbers that multiply to give 24, such as 2 and 12, 3 and 8, and 4 and 6. The factors of 24 are then 1, 2, 3, 4, 6, 8, 12, and 24.
- To find the prime factors of a number, use a factor tree. A factor tree is a diagram that shows how a number can be broken down into smaller factors until only prime factors are left. For example, to find the prime factors of 24, start with 24 at the top of the tree, then branch out two factors that multiply to give 24, such as 2 and 12. Then branch out two factors that multiply to give each of these factors, such as 2 and 6 for 12. Repeat this process until only prime factors are left at the bottom of the tree.
Bonus: Additional 6th Grade number theory worksheets, activities, and resources for reinforcing 6th grader’s math skills
If you want to give your students some extra practice and reinforce their number theory skills, here are some additional worksheets, activities, and resources that you can use:
- Quizizz: Number Theory. This website has a lot of information and examples on various topics in number theory, such as prime numbers, divisibility, factors, multiples, modular arithmetic, and more. It also has interactive quizzes and puzzles to test your students' knowledge and skills. You can find it here: https://quizizz.com/en-in/number-theory-worksheets-class-6.
- Education.com: Number Theory. This website has a comprehensive collection of videos and exercises on number theory, covering topics such as prime factorization, greatest common factor, least common multiple, Euclid's algorithm, the fundamental theorem of arithmetic, and more. It also has a progress tracker and a mastery system to help your students learn at their own pace and level. You can find it here: https://study.com/academy/topic/sba-math-grade-6-number-theory.html.
- Math Goodies: Number Theory. This website has a lot of lessons and worksheets on number theory, such as prime numbers, composite numbers, prime factorization, divisibility rules, greatest common factor, least common multiple, and more. It also has games and puzzles to make learning fun and interactive. You can find it here: https://www.mathgoodies.com/Webquests/number_theory.
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
Number theory is a fascinating and valuable branch of mathematics that can enrich your student's learning experience and prepare them for higher-level math. By teaching number theory to 6th graders, you can help them develop their number sense, logical thinking, problem-solving, and creativity skills. You can use the worksheets, activities, tips, and tricks we shared in this article to make your number theory lessons fun and effective.
You can also visit Mathskills4kids.com or use our recommended resources to find fantastic free and printable 6th Grade number theory worksheets and challenge your kid’s number theory skills. We hope that you have enjoyed this article and found it helpful.
Happy teaching!
