Solving ratios and rates problems in 6th Grade: Tips, Examples, and Worksheets
-
Are you a 6th-grader who wants to learn how to solve ratios and rates problems? Or are you a parent or teacher who wants to help your child or student master this vital math skill? If so, you've come to the right place! In this article, we will provide fun tips, examples, and worksheets that your students can practice daily and are free to download.
Simplify learning ratios and rates: Download Free 6th Grade Worksheets PDF with step-by-step solutions.
Like fractions, this article will help 6th graders learn how to simplify ratios and rates to their lowest forms using a simple step-by-step solution. You can download these free 6th Grade Worksheets PDF from Mathskills4kids.com and start practicing now.
In this article, we'll explain what ratios and rates are, why they are important for 6th-graders, and how to write, represent, compare, and solve them in different ways.
We'll also provide tips, examples, and worksheets to practice and improve your ratios and rates skills. And as a bonus, we'll share some web links with more resources that you can use to learn more about ratios and rates.
So, let's get started!
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
Buying is supporting us!
Buy Now...
-
-
What are ratios and rates?
A ratio compares two quantities of the same kind by division. For example, if 12 boys and 18 girls are in a class, the ratio of boys to girls will be 12:18 or 12/18. A rate is a special ratio that compares two quantities of different kinds by division. For example, if you can run 3 miles in 30 minutes, the rate of your speed is 3 miles per 30 minutes or 3/30.
-
Why are ratios and rates important for 6th-graders?
Ratios and rates are important for 6th-graders because they help them understand the relationships between different quantities and measure how fast or slow something changes.
Ratios and rates also help them solve real-world problems involving proportions, fractions, decimals, percentages, unit conversions, and more.
In addition, ratios and rates are the foundation for learning more advanced math topics such as ratios and proportional relationships, unit rate, unit analysis, scaling, slope, and linear equations.
-
How to write ratios and rates in different ways
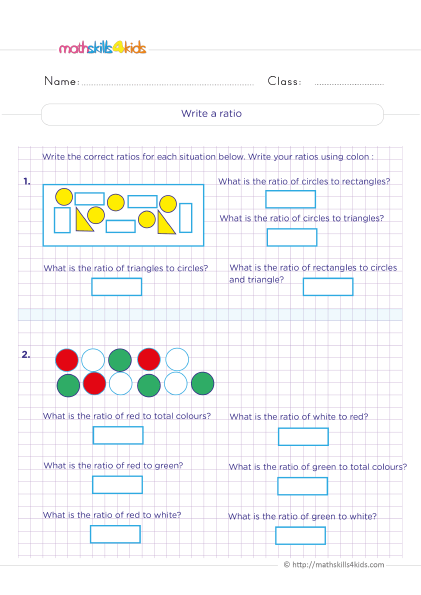
There are three main ways to write ratios and rates: using words, colons (:), or fractions (/). For example, the ratio of boys to girls in a class can be written as:
- "12 boys to 18 girls" using words
- "12:18" using colons
- "12/18" using fractions
The rate of your speed can be written as:
- "3 miles per 30 minutes" using words
- "3:30" using colons
- "3/30" using fractions
We can also simplify ratios and rates by dividing both quantities by a common factor. For example, the ratio of boys to girls in a class can be simplified by dividing both numbers by 6:
- "12 boys to 18 girls" simplifies to "2 boys to 3 girls"
- "12:18" simplifies to "2:3"
- "12/18" simplifies to "2/3"
The rate of your speed can be simplified by dividing both numbers by 3:
- "3 miles per 30 minutes" simplifies to "1 mile per 10 minutes."
- "3:30" simplifies to "1:10"
- "3/30" simplifies to "1/10"
-
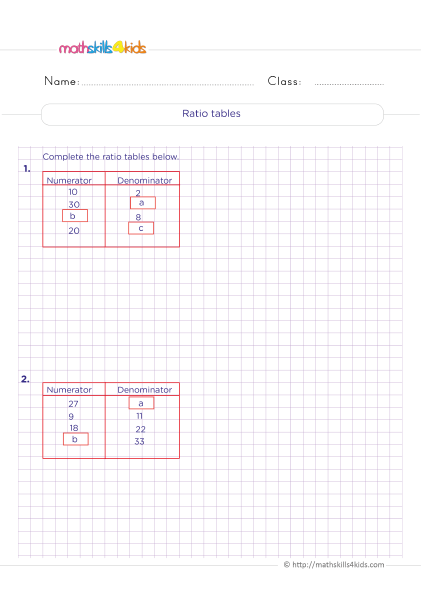
How to find equivalent ratios and simplify rates
Equivalent ratios are ratios that have the same value when simplified. For example, the ratios 2:3, 4:6, and 6:9 are equivalent because they all simplify to 2/3. We can multiply or divide both quantities by the same factor to find equivalent ratios. For example, to find an equivalent ratio to 2:3, we multiply both numbers by 2 to get 4:6 or divide both numbers by 2 to get 1:1.5.
Simplifying rates is similar to simplifying ratios, except that we have to make sure that the units of the quantities are consistent. For example, to simplify the rate of 3 miles per 30 minutes, we will convert the units of distance and time to the same unit, such as miles per hour or minutes per mile. To do this, we can use unit conversions or unit fractions.
For example, to convert 3 miles per 30 minutes to miles per hour, we can multiply by the unit fraction 60 minutes/1 hour, which is equal to 1:
3 miles / 30 minutes x 60 minutes / 1 hour = 180 miles / 1800 minutes = 1 mile / 10 minutes = 6 miles / 60 minutes = 6 miles per hour
-
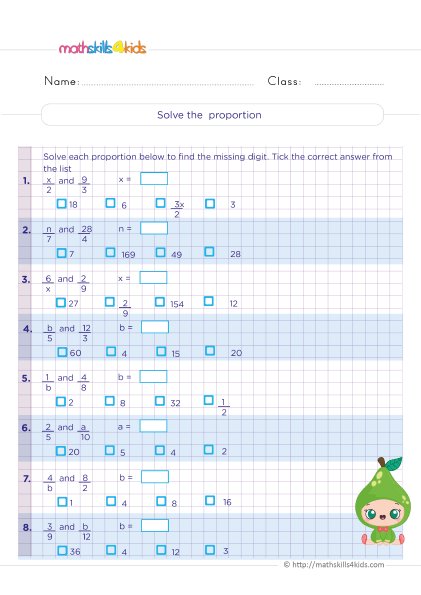
How to compare ratios and rates using cross-multiplication
Cross-multiplication is a method that helps you compare ratios and rates by finding a common denominator. To use cross-multiplication, we will set up a proportion, an equation that states that two ratios or rates are equal. For example, if we want to compare the ratio of boys to girls in two classes, we can write a proportion like this:
12/18 = x/24,
Where x is the number of boys in the second class. Then, we can cross-multiply by multiplying the numerator of one ratio by the denominator of the other ratio and setting them equal. For example:
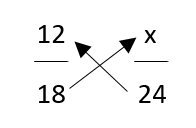
12 x 24 = 18 x (x)
Then, we can solve for x by dividing both sides by 18:
x = (12 x 24) / 18
x = 288 / 18
x = 16
So, the ratio of boys to girls in the second class is 16:24, equivalent to 2:3.
We can also use cross-multiplication to compare rates by ensuring consistent units. For example, if we want to compare the speed of two runners who run different distances at different times, we can write a proportion like this:
3 miles / 30 minutes = x miles / 45 minutes
Where x is the distance run by the second runner. Then, we can cross-multiply and solve for x:
3 x 45 = 30 x x
x = (3 x 45) / 30
x = 135 / 30
x = 4.5
So, the second runner runs 4.5 miles in 45 minutes.
-
How to solve word problems involving ratios and rates
One of the most common applications in 6th Grade math is solving ratios and rates problems. Word problems are mathematical questions that use words and numbers to describe a real-life situation. To solve word problems involving ratios and rates, we can follow these steps:
- Read the problem carefully and identify the given information and the unknown quantity.
- Write a ratio or a rate to represent the relationship between the given information and the unknown quantity.
- Use equivalent ratios, cross-multiplication, or unit rates to find the value of the unknown quantity.
- Check your answer by plugging it back into the ratio or rate and see if it makes sense in the problem context.
- Write a complete sentence to answer the question.
Let's look at examples of applying these steps to different word problems involving ratios and rates.
-
10 ratios and rates word problems with solutions for 6th-Grade
Here are 10-word problems selected from Mathskills4kids.com that your students can practice with to improve their ratios and rates skills in Grade 6. Please encourage them to solve these problems independently, then check the solutions below.
- In a class of 24 students, 18 students like chocolate ice cream, and the rest like vanilla ice cream. What is the ratio of students who like chocolate ice cream to vanilla ice cream? Write your answer in the simplest form.
- A recipe for lemonade calls for 6 cups of water and 1 cup of lemon juice. How many cups of lemon juice are needed to make 18 cups of lemonade?
- A car travels 120 miles in 3 hours. What is the average speed of the car in miles per hour?
- A bag of candy contains 12 red candies, 8 blue candies, and 10 green candies. What is the probability of picking a red candy from the bag?
- A map has a scale of 1 inch: 50 miles. How many inches on the map represent a distance of 300 miles?
- A printer can print 15 pages in 2 minutes. How long will it take to print 60 pages?
- A bag of oranges weighs 12 pounds. If each orange weighs 0.25 pounds, how many oranges are in the bag?
- A bicycle costs $180 and is on sale for 25% off. What is the sale price of the bicycle?
- A cookie recipe makes 24 cookies and uses 2 cups of flour. How many cups of flour are needed to make 36 cookies?
- A painter can paint a wall in 4 hours. How much of the wall can he paint in 1 hour?
Solutions:
- The ratio of students who like chocolate ice cream to vanilla ice cream is 18:6, which can be simplified by dividing both terms by 6, giving 3:1.
- We can use equivalent ratios to find the number of cups of lemon juice needed to make 18 cups of lemonade. If 6 cups of water and 1 cup of lemon juice make one batch of lemonade, then we can multiply both terms by 3 to get another equivalent ratio: 18 cups of water and 3 cups of lemon juice make three batches of lemonade.
Therefore, we need 3 cups of lemon juice to make 18 cups of lemonade.
- To find the average speed of the car in miles per hour, we can use a unit rate, which is a rate that compares a quantity to one unit of another quantity. In this case, we want to compare miles to one hour, so we divide both terms by the time:
120 miles / 3 hours = 40 miles/hour
The average speed of the car is 40 miles per hour.
- To find the probability of picking a red candy from the bag, we can use a ratio that compares the number of favorable outcomes to the total number of possible outcomes. In this case, the number of favorable outcomes is the number of red candies, which is 12, and the total number of possible outcomes is the number of all candies, which is 12 + 8 + 10 = 30. The ratio is then:
12 / 30 = 0.4
The probability of picking a red candy from the bag is 0.4 or 40%.
- We can use equivalent ratios again to find how many inches on the map represent a distance of 300 miles. If one inch on the map represents 50 miles in reality, then we can multiply both terms by x to get another equivalent ratio:
x inches on the map represent 300 miles in reality.
Then, we can solve for x by cross-multiplying:
1 x 300 = (x) x 50
x = (1 x 300) /50
x = 6
Therefore, 6 inches on the map represents a distance of 300 miles.
- We can use another unit rate to find how long it will take to print 60 pages. If the printer can print 15 pages in 2 minutes, then we can divide both terms by 15 to get a unit rate that compares pages to one minute:
15 pages / 2 minutes = 1 page / (2/15) minutes
The printer can print one page in (2/15) minutes, equivalent to 0.133 minutes or 8 seconds. To print 60 pages, we can multiply both terms by 60:
1 page / (2/15) minutes = 60 pages / (120/15) minutes
The printer can print 60 pages in (120/15) minutes, equivalent to 8 minutes.
- To find how many oranges are in the bag, we can use a rate that compares the bag's weight to the number of oranges. The rate is:
12 pounds / x oranges
To find x, we can use the fact that each orange weighs 0.25 pounds, which means that x oranges weigh x x 0.25 pounds. We can then set up an equation and solve for x:
12 pounds = x x 0.25 pounds
x = 12 / 0.25
x = 48
There are 48 oranges in the bag.
- To find the sale price of the bicycle, we can use a percentage, which is a ratio that compares a part to a whole and is expressed as a fraction of 100. In this case, the part is the discount amount, and the whole is the original price of the bicycle. The percentage is:
25% = 25 / 100 = 0.25
To find the amount of discount, we can multiply the percentage by the original price:
0.25 x $180 = $45
The amount of discount is $45. To find the sale price, we can subtract the amount of discount from the original price:
$180 - $45 = $135
The sale price of the bicycle is $135.
- To find how many cups of flour are needed to make 36 cookies, we can use a proportion, which is an equation that states that two ratios are equal. In this case, the two ratios are:
2 cups of flour / 24 cookies = x cups of flour / 36 cookies
To find x, we can cross-multiply and solve for x:
2 x 36 = (x) x 24
x = (2 x 36) /24
x = 3
We need 3 cups of flour to make 36 cookies.
- We can use another proportion to find how much of the wall he can paint in one hour. The two ratios are:
1 wall / 4 hours = x wall / 1 hour
To find x, we can cross-multiply and solve for x:
1 x 1 = (x) x4
x = (1 x 1) /4
x = 0.25
He can paint 0.25 or one-fourth of the wall in one hour.
Bonus: More resources for solving ratios and rates problems in 6th Grade
If you want more practice for your 6th graders on solving ratios and rates problems, then check out these web links:
- https://www.khanacademy.org/math/cc-sixth-grade-math/cc-6th-ratios-prop/cc-6th-ratios-intro/v/ratios-intro
This video from Khan Academy introduces the concept of ratios and how to write them in different ways.
- https://www.mathsisfun.com/numbers/ratio.html
This webpage from Math is Fun explains what ratios are and how to use them in various situations.
- https://www.mathplayground.com/index.html?category=ratios_and_proportions
This webpage from Math Playground has interactive games and activities that help 6th graders practice ratios and proportions.
- https://www.ixl.com/math/grade-6/solve-word-problems-involving-unit-rates
This webpage from IXL has online exercises with unit-rate word problems for Grade 6.
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion: the benefits of mastering ratios and rates in everyday situations
Your 6th-grade students have learned much about ratios and rates in this article. They have seen how to write them in different ways, how to use tables, graphs, and diagrams to represent them, how to find equivalent ratios and simplify rates, how to compare them using cross-multiplication, and how to solve word problems involving them. They have also practiced their skills with 10 ratios and rates word problems with solutions for 6th grade.
But why are ratios and rates important to us? How can they help us in our daily life? Here are some examples of how we can use ratios and rates in everyday situations:
- Cooking: We can use ratios and rates to measure ingredients, adjust recipes, compare prices, and calculate nutritional values. For example, if we want to make a cake that serves 12 people, but the recipe is for 8 people, we can use a ratio to determine how much each ingredient is needed.
- Sports: We can use ratios and rates to analyze performance, compare players, and predict outcomes. For example, if we want to compare two basketball players, we can use ratios to compare their points, rebounds, assists, and other statistics.
- Art: We can use ratios and rates to create designs, patterns, and proportions. For example, if we want to draw a face, we can use ratios to divide the head into sections and place the features accordingly.
- Science: We can use ratios and rates to explore nature, conduct experiments, and interpret data. For example, if we want to know how many birds are in a park, we can use a ratio to compare the number of birds we see in a sample area to the total park area.
As we can see, ratios and rates are useful for many aspects of our lives. They help us make sense of the world around us and solve problems creatively.
By mastering ratios and rates in 6th grade, your students will be ready for more advanced math topics in the future. They will also develop critical thinking skills that benefit them in school and beyond.