6th Grade mixed numbers and fractions worksheets
Hello! Prepare to embark on a fun-filled math journey that will leave your child eager to solve more fraction problems and excel in their mathematical abilities. This article will provide well-structured 6th Grade mixed numbers and fractions worksheets that you can use to teach 6th graders the fundamental rules, tips, and tricks for simplifying and comparing mixed numbers and fractions easily.
-
Learn, practice, and master mixed numbers and fractions in 6th Grade with these amazing worksheets.
Do your 6th-grade students need help grasping the concept of mixed numbers and fractions? Look no further! We have the perfect solution for you. Visit Mathskills4kids.com and download amazing worksheets that make learning, practicing, and mastering mixed numbers and fractions in 6th grade easy and fun.
With clear explanations and step-by-step instructions, your students will become fractions experts in no time. Each worksheet is carefully crafted to provide a hands-on learning experience, allowing learners to apply their knowledge and reinforce their understanding.
Whether your 6th graders are just starting or need extra practice, our worksheets are tailored to suit their needs. Say goodbye to confusion and hello to confidence with our comprehensive collection of 6th Grade mixed numbers and fractions worksheets.
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
-
How to place fractions on a number line
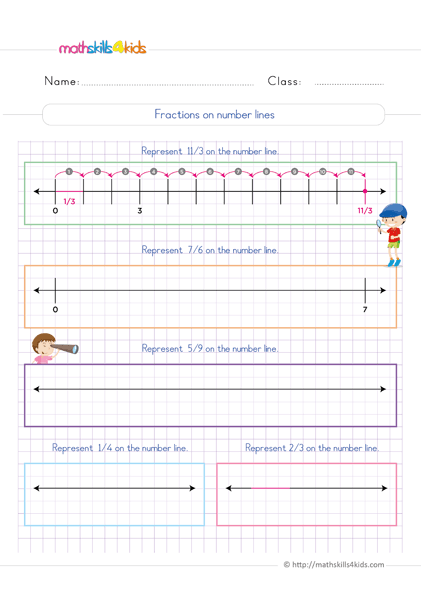 Print it...
Print it...
-
How to find the least common denominator
 Print it...
Print it...
-
Compare fractions with like and unlike denominator
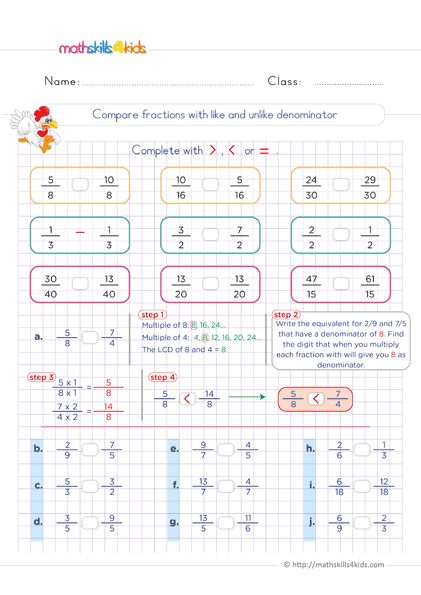 Print it...
Print it...
-
Comparing fractions word numbers
 Print it...
Print it...
-
Ordering fractions and decimals
 Print it...
Print it...
-
Understanding fractions as division word-problems
 Print it...
Print it...
-
How to place fractions on a number line
-
Buying is supporting us!
Buy Now...
-
-
Understanding mixed numbers and fractions
Mixed numbers and fractions are two ways of representing parts of a whole. A mixed number consists of a whole and a fraction, such as 2 1/4. A fraction consists of a numerator (the top number) and a denominator (the bottom number), such as 3/5.
Both mixed numbers and fractions can be used to compare, order, add, subtract, multiply, and divide quantities.
-
Why learning mixed numbers and fractions is important
Learning mixed numbers and fractions is essential for several reasons. First, mixed numbers and fractions help us to express measurements that are not whole numbers, such as lengths, weights, volumes, and time. For example, we can use mixed numbers to measure a person's height (5 1/2 feet) or the weight of a fruit (1 3/4 pounds). We can use fractions to measure the amount of liquid in a cup (3/4 cup) or the duration of an activity (1/2 hour).
Secondly, mixed numbers and fractions help us understand ratios and proportions, which are essential for solving problems involving scale, similarity, rates, and percentages. For example, we can use fractions to compare the sizes of different shapes (a square with a side length of 3/4 inch is similar to a square with a side length of 9/12 inch) or the speeds of different vehicles (a car that travels 60 miles in 3/4 hour has the same rate as a car that travels 80 miles in 1 hour).
Third, mixed numbers and fractions help us develop algebraic thinking and reasoning skills for solving equations and inequalities, manipulating expressions, and modeling situations. For example, we can use fractions to simplify expressions (2/4 + 3/4 = 5/4) or to solve equations (x/3 = 2/5).
-
How to teach mixed numbers and fractions to 6th Graders
Teaching mixed numbers and fractions to 6th graders can be challenging but rewarding. Here are some tips on how to teach mixed numbers and fractions effectively:
- Use concrete materials and visual representations to introduce and reinforce the concepts of mixed numbers and fractions. For example, you can use fraction strips, fraction circles, number lines, area models, or bar models to show how mixed numbers and fractions are related to each other and whole numbers.
- Use real-world contexts and examples to make mixed numbers and fractions relevant and meaningful for students. For example, you can use recipes, sports scores, surveys, or maps to show how mixed numbers and fractions are used in everyday situations.
- Use games, puzzles, songs, or stories to make mixed numbers and fractions fun and engaging for students. For example, you can use bingo cards, dominoes, memory cards, or dice to practice identifying, comparing, or converting mixed numbers and fractions. You can also use songs or stories that involve mixed numbers and fractions to spark students' interest and curiosity.
- Use scaffolding and differentiation strategies to meet student's diverse needs and abilities. For example, you can use graphic organizers, manipulatives, or calculators to support students who struggle with mixed numbers and fractions. You can also use extensions, challenges, or projects to enrich students who excel with mixed numbers and fractions.
-
Common misconceptions about mixed numbers and fractions
Some common misconceptions that students may have about mixed numbers and fractions are:
- Thinking that a larger denominator means a larger fraction. For example, some students may think 3/8 is larger than 2/5 because 8 is larger than 5. However, this is not true because the numerator also affects the size of the fraction.
We need to find equivalent fractions with the same denominator or convert them to decimals to compare fractions with different denominators.
- Thinking that adding or subtracting the numerators and denominators separately is the correct way to add or subtract fractions. For example, some students may think that 2/3 + 1/4 = 3/7 because they add 2 + 1 = 3 and 3 + 4 = 7. However, this is false because we must find a common denominator before adding or subtracting fractions. The correct way is to rewrite 2/3 as 8/12 and 1/4 as 3/12 and then add them as 8/12 + 3/12 = 11/12.
- Thinking that multiplying or dividing the numerators and denominators separately is the correct way to multiply or divide fractions. For example, some students may think that 2/3 x 1/4 = 2/12 because they multiply 2 x 1 = 2 and 3 x 4 = 12. However, this is false because we must simplify the fraction before or after multiplying or dividing fractions. The correct way is to multiply 2/3 x 1/4 = 2/12 and then simplify it as 1/6.
- Thinking that a larger denominator means a larger fraction. For example, some students may think 3/8 is larger than 2/5 because 8 is larger than 5. However, this is not true because the numerator also affects the size of the fraction.
-
Practicing converting mixed numbers to improper fractions
One skill students need to master when working with mixed numbers and fractions is converting mixed numbers to improper fractions. An improper fraction is a fraction where the numerator is larger than or equal to the denominator, such as 7/4 or 5/5. To convert a mixed number to an improper fraction, we need to follow these steps:
- Multiply the whole number by the denominator of the fraction.
- Add the result to the numerator of the fraction.
- Write the sum as the new numerator over the same denominator.
For example, to convert 2 1/4 to an improper fraction, we:
- Multiply 2 by 4 and get 8.
- Add 8 to 1 and get 9.
- Write 9 as the new numerator over 4 as the same denominator.
So, 2 1/4 = 9/4 as an improper fraction.
-
Practicing converting improper fractions to mixed numbers
Another skill that students need to master when working with mixed numbers and fractions is converting improper fractions to mixed numbers. A mixed number is a number that consists of a whole number and a fraction, such as 2 1/4 or 3 3/5. To convert an improper fraction to a mixed number, we need to follow these steps:
- Divide the numerator by the denominator and get the quotient and the remainder.
- Write the quotient as the whole number and the remainder as the numerator over the same denominator.
For example, to convert 9/4 to a mixed number, we:
- Divide 9 by 4 and get 2 as the quotient and 1 as the remainder.
- Write 2 as the whole number and 1 as the numerator over 4 as the same denominator.
So, 9/4 = 2 1/4 as a mixed number.
-
Practicing addition and subtraction with mixed numbers and fractions
One of the most essential skills for 6th graders to master is adding and subtracting mixed numbers and fractions. This skill will help them solve complex problems involving fractions, decimals, and percentages. To practice addition and subtraction with mixed numbers and fractions, students need to follow these steps:
- Convert any mixed numbers to improper fractions. To do this, multiply the whole number by the denominator and add the numerator. For example, 2 1/4 becomes 9/4.
- Find the lowest common denominator (LCD) of the fractions. To do this, find the denominators' least common multiple (LCM). For example, the LCD of 9/4 and 3/8 is 8 because the LCM of 4 and 8 is 8.
- Rewrite the fractions with the LCD as their new denominator. To do this, multiply the numerator and denominator by the same factor. For example, 9/4 becomes 18/8, and 3/8 stays the same.
- Add or subtract the fractions' numerators and write the result over the LCD. For example, 18/8 + 3/8 = 21/8 and 18/8 - 3/8 = 15/8.
- Simplify the fraction, if possible, by dividing the numerator and denominator by a common factor. For example, 21/8 becomes 2 5/8 and 15/8 becomes 1 7/8.
- Convert any improper fractions to mixed numbers if needed. To do this, divide the numerator by the denominator and write the quotient as the whole number and the remainder as the numerator over the denominator. For example, 21/8 becomes 2 5/8.
To help students practice these steps, teachers can use Mathskills4kids’ worksheets that provide different problems involving addition and subtraction with mixed numbers and fractions. Some examples are:
- Adding or subtracting two mixed numbers
- Adding or subtracting two fractions
- Adding or subtracting a mixed number and a fraction
- Adding or subtracting three or more mixed numbers or fractions
- Solving word problems that involve addition or subtraction with mixed numbers or fractions
Teachers can also use manipulatives, such as fraction strips, fraction circles, or number lines, to help students visualize and compare mixed numbers and fractions.
-
Practicing multiplication and division with mixed numbers and fractions
Another essential skill for 6th graders to master is multiplying and dividing mixed numbers and fractions. This skill will help them solve more advanced problems involving ratios, proportions, and rates. To practice multiplication and division with mixed numbers and fractions, students need to follow these steps:
- Convert any mixed numbers to improper fractions using the same method as in addition and subtraction.
- For multiplication, multiply the fractions' numerators and write the product over the product of the denominators. For example, 9/4 x 3/8 = 27/32.
- For division, invert (flip) the second fraction and multiply it by the first fraction. For example, 9/4 ÷ 3/8 = 9/4 x 8/3 = 72/12.
- Simplify the fraction, if possible, using the same method as in addition and subtraction.
- Convert any improper fractions to mixed numbers using the same method as in addition and subtraction.
To help students practice these steps, teachers can use Mathskills4kids’ worksheets that provide multiplication and division problems with mixed numbers and fractions. Some examples are:
- Multiplying or dividing two mixed numbers
- Multiplying or dividing two fractions
- Multiplying or dividing a mixed number and a fraction
- Multiplying or dividing three or more mixed numbers or fractions
- Solving word problems that involve multiplication or division with mixed numbers or fractions
Teachers can also use manipulatives, such as fraction strips, fraction circles, or number lines, to help students visualize and compare mixed numbers and fractions.
-
Tips and Tricks for simplifying and comparing mixed numbers and fractions
Simplifying and comparing mixed numbers and fractions are essential skills for working with these types of numbers. Simplifying means reducing a fraction to its lowest terms by dividing the numerator and denominator by a common factor. Comparing means determining which fraction is larger, smaller, or equal to another fraction by finding a common denominator or using cross-multiplication.
Here are some tips and tricks for simplifying and comparing mixed numbers and fractions:
- To simplify a fraction quickly, look for common factors in the numerator and denominator that can be divided. For example, to simplify 12/18, you can divide both by 2 to get 6/9, then by 3 to get 2/3.
- To compare two fractions with the same denominator, look at the numerators and see which is larger or smaller. For example, to compare 3/8 and 5/8, you can see that 5/8 is larger because 5 is larger than 3.
- To compare two fractions with different denominators, find the lowest common denominator (LCD) and rewrite the fractions with the LCD as their new denominator. Then compare the numerators as before.
For example, to compare 2/3 and 3/4, you can find the LCD to be 12 and rewrite the fractions as 8/12 and 9/12. Then you can see that 9/12 is larger than 8/12.
- Another way to compare two fractions with different denominators is to use cross-multiplication. This means multiplying the numerator of one fraction by the denominator of the other fraction and comparing the products.
For example, to compare 2/3 and 3/4, you can cross-multiply and get 2 x 4 = 8 and 3 x 3 = 9. Then you can see that 9 is larger than 8, so 3/4 is larger than 2/3.
- To compare a mixed number and a fraction, convert the mixed number to an improper fraction and compare as before. For example, to compare 2 1/4 and 7/8, you can convert 2 1/4 to 9/4 and compare it with 7/8 using either the LCD or cross-multiplication method.
To help students practice these tips and tricks, teachers can use Mathskills4kids’ worksheets that provide different problems involving simplifying and comparing mixed numbers and fractions. Some examples are:
- Simplifying mixed numbers or fractions
- Comparing two mixed numbers or fractions using <, >, or =
- Ordering three or more mixed numbers or fractions from least to greatest or greatest to least
- Finding equivalent fractions or mixed numbers
- Finding the simplest form of a fraction or mixed number
Teachers can also use manipulatives, such as fraction strips, fraction circles, or number lines, to help students visualize and compare mixed numbers and fractions.
-
6th Grade mixed numbers and fractions word problems
Word problems are a great way to apply the skills of working with mixed numbers and fractions to real-world situations. Word problems can involve any of the four operations (addition, subtraction, multiplication, or division) and simplifying and comparing mixed numbers and fractions.
Here are some examples of 6th-grade mixed numbers and fractions word problems available at Mathskills4kids.com:
- Anna baked a cake and cut it into 12 equal pieces. She ate 2 pieces and gave 3 pieces to her friend. What fraction of the cake did she have left?
- Ben ran a marathon in 3 hours and 15 minutes. He ran the first half of the marathon in 1 hour and 45 minutes. What fraction of the marathon did he run in the second half?
- Claire has a recipe that calls for 2 cups of flour, but she only has a measuring cup that holds 1/4 cup. How often does she need to fill the measuring cup to get the right amount of flour?
- David bought a pizza that was cut into 8 slices. He ate 3 slices, and his brother ate 2 slices. What fraction of the pizza did they eat together? What fraction of the pizza was left?
- Emma has a bag of candy that contains 20 pieces. She gave away half of the candy to her friends. Then she ate one-fourth of what was left. How many pieces of candy did she have left?
To help students practice these word problems, teachers can use our worksheets that provide problems involving mixed numbers and fractions in various contexts. Teachers can also encourage students to create their word problems using mixed numbers and fractions.
Bonus: additional resources for mastering mixed numbers and fractions in 6th grade
If you want to learn more about mixed numbers and fractions, or if you need some extra practice, here are some helpful web links that you can check out for more 6th Grade mixed numbers and fractions worksheets, videos, games, lessons, etc.:
- Khan Academy: This website has video lessons, interactive exercises on mixed numbers and fractions, and other math topics. Students can learn at their own pace and track their progress. https://www.khanacademy.org/math/arithmetic/fraction-arithmetic.
- Math Playground: This website has fun and engaging games for practicing mixed numbers, fractions, and other math concepts. Students can play against the computer or with a friend. https://www.mathplayground.com/index_fractions.html.
- IXL: This website has adaptive practice questions on mixed numbers, fractions, and other math topics. You can get instant feedback and earn awards as you improve your skills. https://www.ixl.com/math/grade-6.
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
Mixed numbers and fractions are essential concepts to master in 6th-grade math. They help students understand parts of a whole, compare quantities, and perform operations with rational numbers.
By learning how to convert, add, subtract, multiply, and divide mixed numbers and fractions, your 4 6th Grade math lovers can solve various math and real-life problems in less than no time.
We hope this article has helped your learners better understand mixed numbers and fractions and that you have enjoyed our activities and worksheets.
Remember to practice regularly with your 6th graders and use the additional resources suggested if they need more help. Happy learning!
