Grade 5 math worksheets: Identifying and classifying triangles & quadrilaterals
Welcome to our enriched math article on Grade 5 math worksheets: identifying and classifying triangles and quadrilaterals.
-
In this article, we will explain what triangles and quadrilaterals are, why they are essential for 5th-graders to learn, how to identify and classify them by their sides and angles, how to find their perimeter and area, and how to solve word problems involving triangles and perimeter. We will also provide review and practice questions and bonus learning resources for 5th-graders who want to explore more about triangles and quadrilaterals.
Teaching fifth graders about triangles and quadrilaterals with fun and engaging math worksheets
Teaching fifth graders about triangles and quadrilaterals can be daunting, but with fun and engaging math worksheets, your child will become a pro in no time. In line with this, we will introduce you to MathSkills4Kids.com, a fantastic website offering hundreds of free printable Grade 5 math worksheets covering all Grade 5 math curriculum concepts.
However, apart from Mathskills4kids.com, we will provide more triangles and quadrilaterals learning resources and websites for 5th graders. Let's get started!
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
5th GRADE MATH TOPICS
- Number sense
- Addition and subtraction
- Multiplication
- Division
- Exponents
- Number theory
- Decimals
- Add & subtract decimals
- Multiply decimals
- Divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Mixed operations
- Problems solving
- Ratios and rates
- Percentages
- Money Math
- Number sequences
- Coordinate graph
- Variable expressions
- Data and Graphs
- Probability and statistics
- Telling time
- Unit of measurements
- 2D figures
- Triangles & quadrilaterals
- Symmetry & transformations
- 3D figures
- Geometric measurements
-
-
How do you know if a triangle is acute obtuse or right?
 Print it...
Print it...
-
Classifying riangles - Equilateral, isosceles and scalene
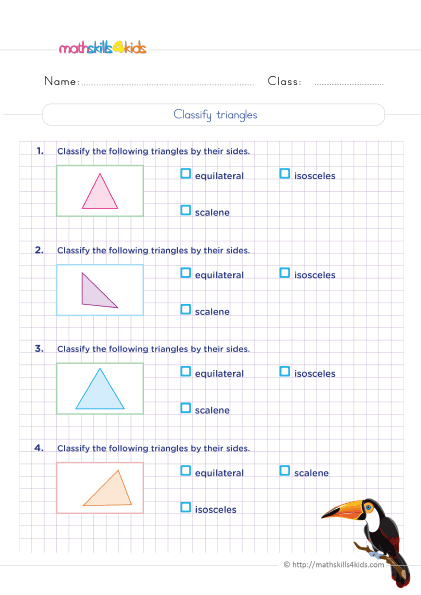 Print it...
Print it...
-
How do you find the missing angle of a triangle?
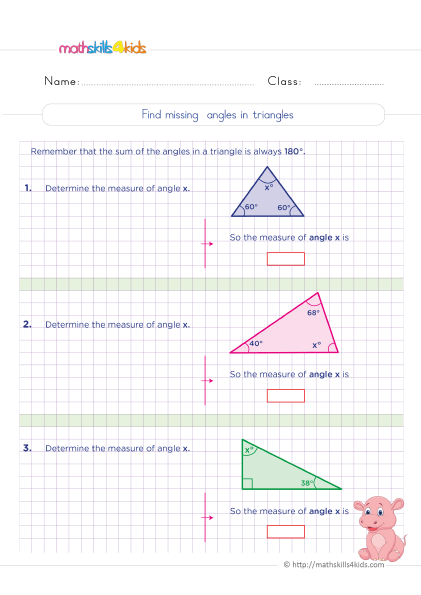 Print it...
Print it...
-
Identifying trapezoids - Trapezoid properties
 Print it...
Print it...
-
Identifying rhombuses
 Print it...
Print it...
-
Classifying quadrilaterals practice
 Print it...
Print it...
-
How do you know if a triangle is acute obtuse or right?
-
Buying is supporting us!
Buy Now...
-
-
What are triangles and quadrilaterals?
Triangles and quadrilaterals are two types of polygons, closed shapes made of straight lines. A triangle is a polygon with three sides and three angles, while a quadrilateral has four sides and four angles. Here are some examples of triangles and quadrilaterals:
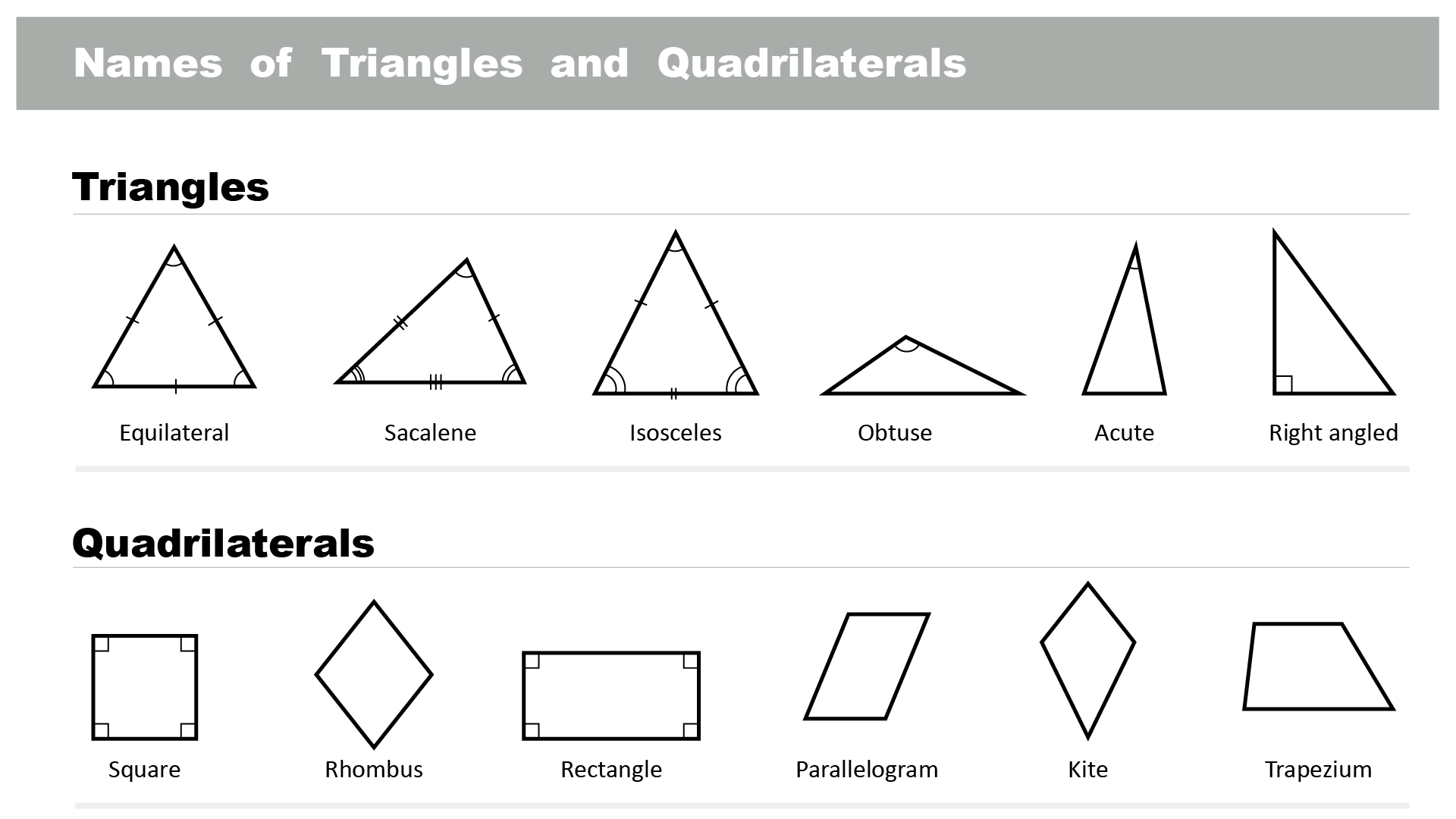
-
Why triangles and quadrilaterals math skills are important to 5th-Graders
For several reasons, mastering triangles and quadrilaterals skills are important for 5th graders in math and their daily lives. Triangles and quadrilaterals are common shapes we see in everyday life, such as buildings, art, nature, and sports.
First, learning about triangles and quadrilaterals can help 5th-graders develop their spatial reasoning skills, which are the ability to visualize and manipulate shapes in two-dimensional and three-dimensional space. Spatial reasoning skills are essential for many fields of study and careers, such as engineering, architecture, design, art, science, and technology.
Secondly, learning about triangles and quadrilaterals can help 5th-graders improve their geometry skills, which are the study of shapes, sizes, positions, and properties of figures. Geometry skills are important for understanding measurement, symmetry, congruence, similarity, transformations, patterns, and coordinate systems.
Geometry skills can also help 5th-graders solve problems in other areas of math, such as algebra, fractions, decimals, percentages, ratios, proportions, and statistics.
-
How to identify triangles by their sides and angles
There are different ways to identify triangles by their sides and angles. One way is to look at the length of the sides. Based on the length of the sides, we can classify triangles into three types:
- Equilateral triangle: A triangle with all three sides equal in length.
- Isosceles triangle: A triangle with two sides equal in length.
- Scalene triangle: A triangle with no sides equal in length.
Another way is to look at the measure of the angles. Based on the measure of the angles, we can classify triangles into three types:
- Acute triangle: A triangle with all three angles less than 90 degrees.
- Right triangle: A triangle with one angle equal to 90 degrees.
- Obtuse triangle: A triangle with one angle greater than 90 degrees.
We can also combine the two ways to identify triangles by their sides and angles. For example, we can have an equilateral acute triangle, an isosceles right triangle, or a scalene obtuse triangle.
Here is a table that summarizes the different types of triangles by their sides and angles:
Isosceles triangle
equilateral triangle
Scalene triangle
Right triangle
Obtuse triangle
Acute triangle
2 equal sides
All equal sides
No equal side
Only one right angle of 900
1 angle greater than 900
All angles are less than 900
-
How to identify quadrilaterals by their sides and angles
Similar to triangles, there are different ways to identify quadrilaterals by their sides and angles. One way is to look at the parallelism of the sides. Based on the parallelism of the sides, we can classify quadrilaterals into two types:
- Parallelogram: A quadrilateral with both pairs of opposite sides parallel.
- Trapezoid: A quadrilateral with only one pair of opposite sides parallel.
Another way is to look at the equality of the sides. Based on the equality of the sides, we can classify parallelograms into three types:
- Rectangle: A parallelogram with all four sides equal in length.
- Rhombus: A parallelogram with all four angles equal in measure.
- Square: A parallelogram with four sides equal in length and four angles equal in measure.
We can also classify trapezoids into two types based on the equality of the non-parallel sides:
- Isosceles trapezoid: A trapezoid with both non-parallel sides equal in length.
- Scalene trapezoid: A trapezoid with no sides equal in length.
Here is a table that summarizes the different types of quadrilaterals by their sides and angles:
Quadrilaterals
Sides
Angles
Parallelogram
- Two pairs of equal sides
- Opposing sides are parallel
Two opposing pairs of equal angles
Trapezoid
- One pair of parallel sides
No equal angle
Rectangle
- Two pairs of equal sides
- Opposing sides are parallel
All equal angles (900)
Rhombus
- Four equal sides
- Opposing sides are parallel
Two opposing pairs of equal angles
Square
- Four equal sides
- Opposing sides are parallel
All equal angles (900)
Isosceles trapezoid
- One pair of equal sides
- One pair of parallel sides
Two pairs of equal angles
Scalene trapezoid
- No equal sides
- One pair of parallel sides
No equal angle
-
How to classify triangles and quadrilaterals into different types
Now that we know how to identify triangles and quadrilaterals by their sides and angles, we can use a classification process to sort them into different types. Classification is grouping objects based on their common characteristics or properties. Classification can help us organize information, compare and contrast objects, and make generalizations and predictions.
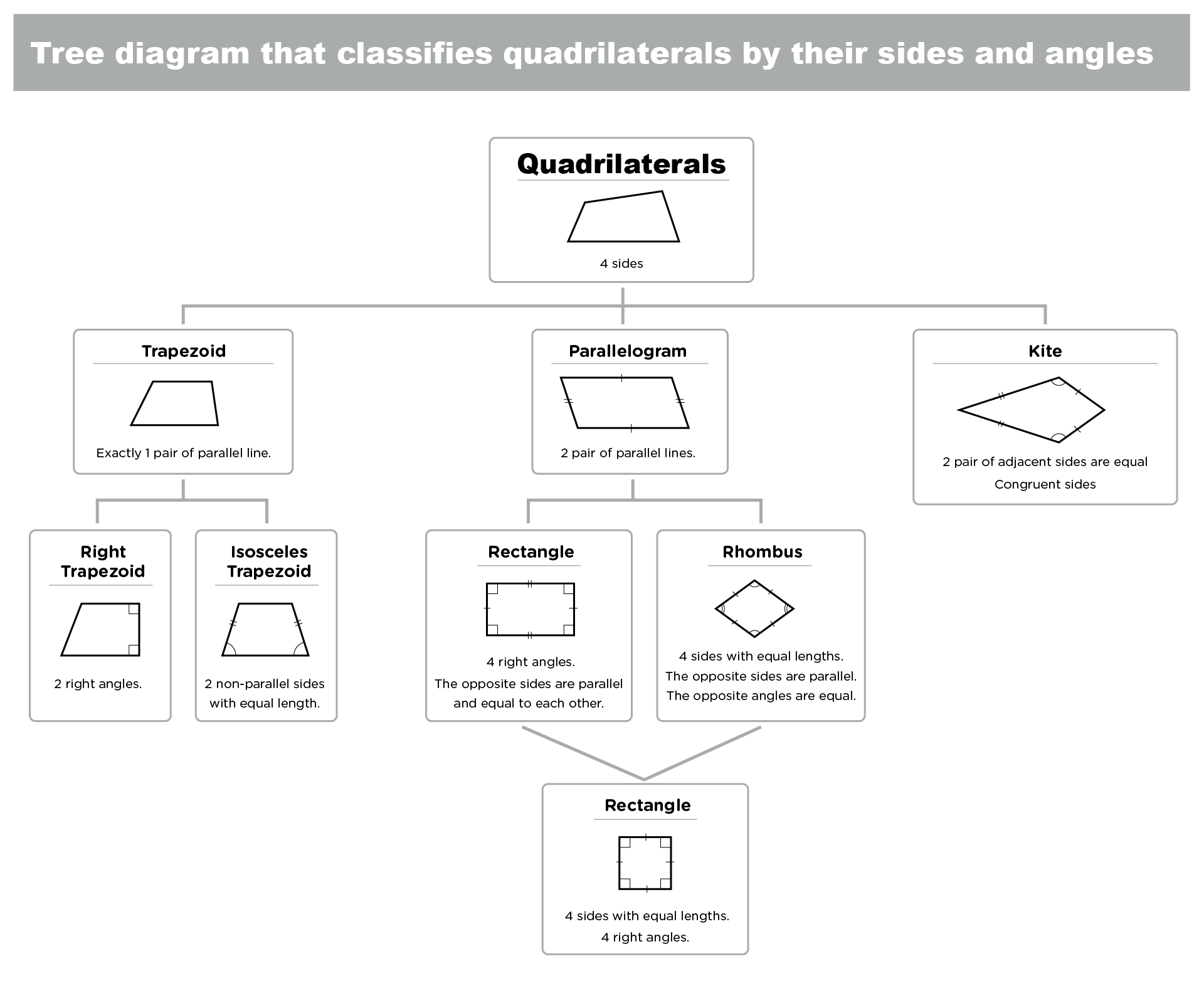
To classify triangles and quadrilaterals into different types, we can use a tree diagram, i.e., a visual representation of the hierarchical relationship between different types of objects. A tree diagram starts with a general category at the top and then branches into more specific subcategories at lower levels. Each subcategory inherits the properties of its parent category and adds more specific properties of its own.
Here is an example of a tree diagram that classifies triangles by their sides and angles:
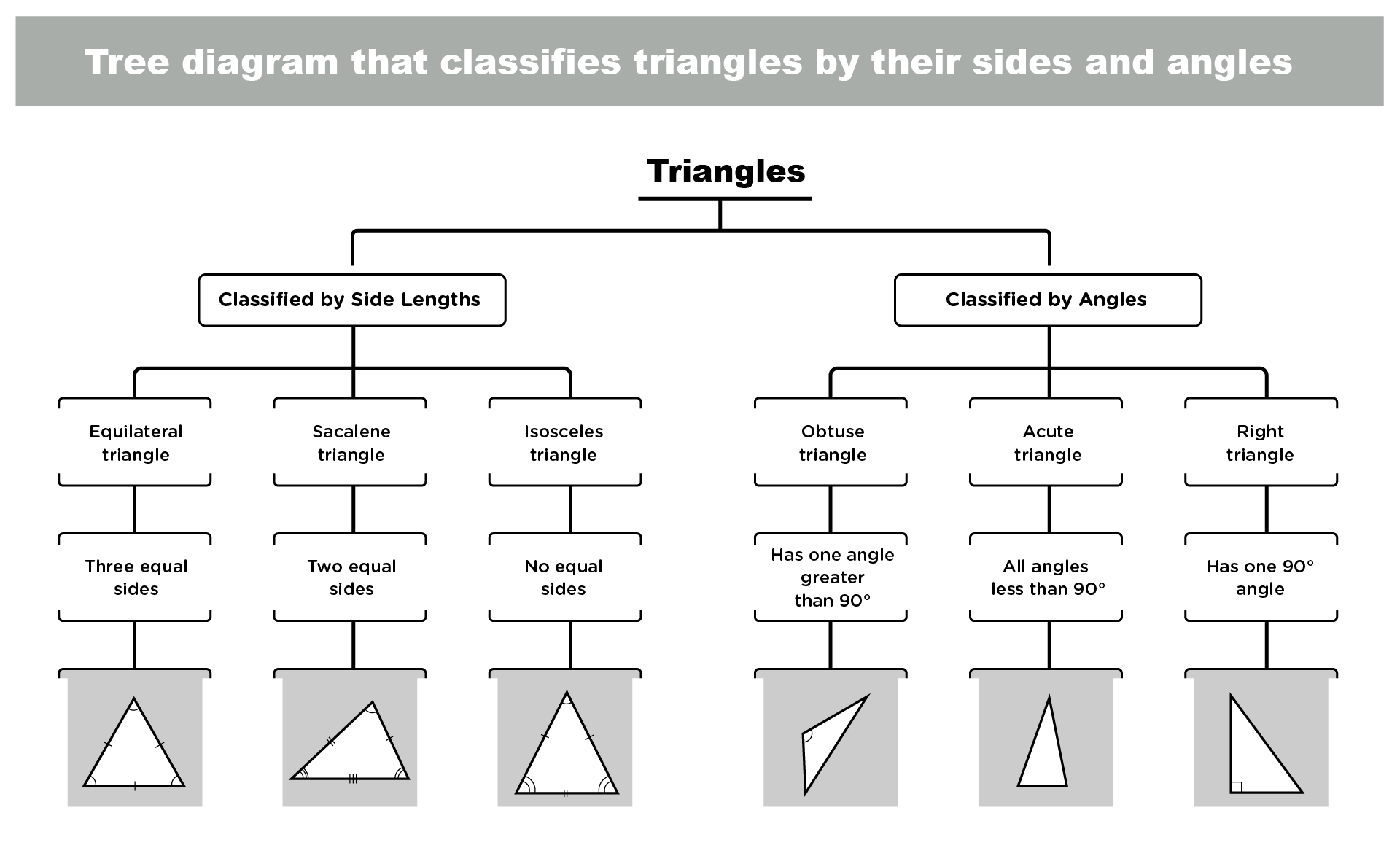
Here is an example of a tree diagram that classifies quadrilaterals by their sides and angles:
-
How to find the perimeter and area of triangles and quadrilaterals
Another vital skill for 5th graders is finding the perimeter and area of triangles and quadrilaterals. The perimeter is the distance around the edge of a shape, while the area is the amount of space inside a shape. Finding the perimeter and area of triangles and quadrilaterals can help us measure their size, compare their shapes, and calculate their cost, efficiency, or capacity.
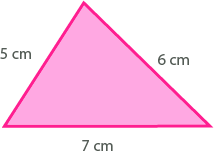
To find the perimeter of a triangle or a quadrilateral, we can use a simple formula: add up the lengths of all the sides. For example, to find the perimeter of this triangle, we can add up 5 cm + 6 cm + 7 cm = 18 cm.
To find the area of a triangle or a quadrilateral, we need to use different formulas depending on their type. Here are some common formulas for finding the area of triangles and quadrilaterals:
- Area of a triangle = (base x height) / 2
- Area of a rectangle = length x width
- Area of a square = side x side
- Area of a parallelogram = base x height
- Area of a trapezoid = (base 1 + base 2) x height / 2
- Area of a rhombus = (diagonal 1 x diagonal 2) / 2
-
How to solve word problems involving triangles and quadrilaterals
One way to apply our knowledge of triangles and quadrilaterals is to solve word problems involving them. Word problems are math problems that use words to describe a situation or scenario. To solve word problems involving triangles and quadrilaterals, we need to follow these steps:
- Read the problem carefully and identify what is given and what is asked.
- Draw a diagram or sketch to represent the problem.
- Label the diagram with the given information and variables.
- Write an equation or formula that relates the given information and the unknown variable.
- Solve the equation or formula for the unknown variable.
- Check your answer by plugging it back into the equation or formula.
- Write your answer in a complete sentence with appropriate units.
Bonus: More triangles and quadrilaterals learning resources for 5th-Graders
If you want your 5th graders to learn more about identifying and classifying triangles and quadrilaterals or practice their skills with some fun and interactive activities, here are some websites that you can check out:
- https://www.mathsisfun.com/triangle.html: This website has a lot of information and examples about triangles, such as how to measure angles, how to find the height, how to use the Pythagorean theorem and more. Students can also play some games and quizzes to test their knowledge.
- https://www.mathsisfun.com/geometry/quadrilaterals.html: This website helps 5th Grade students to learn about the properties and types of quadrilaterals, how to find the area and perimeter, how to draw them on a grid, and more. They can also try some puzzles and challenges to practice their skills.
- https://www.khanacademy.org/math/geometry-home/quadrilaterals-and-polygons: This website has a series of videos and exercises that cover the 5th-grade geometry topics, including triangles and quadrilaterals. Students can watch the videos to learn the concepts and then practice them with the exercises. They can also track your progress and earn badges as they go.
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
In this article, we learned about triangles and quadrilaterals, how to identify and classify them by their sides and angles, how to find their perimeter and area, and how to solve word problems involving them. We also learned why these skills are important for 5th-graders and how they can help us in real-life situations.
Triangles and quadrilaterals are everywhere around us. They are used in architecture, engineering, art, design, sports, games, and more. By knowing how to work with them, students can understand how things are built, how they function, how they look, and how they can be improved.
For example, we can use triangles to measure distances or heights that are hard to reach, such as the height of a building or a mountain. We can use quadrilaterals to design floor plans or maps that show the dimensions and shapes of rooms or areas. We can also use triangles and quadrilaterals to create beautiful patterns or artworks with symmetry or balance.
We hope your 5th graders enjoyed this article and learned something new. If you have any questions or comments, you can comment below. Thank you for reading!
