Solving two-variable equations worksheets for 6th Graders
-
Do you want your 6th grader to easily learn to solve equations with two variables, such as x and y? Do you want them to practice their skills with fun and engaging worksheets? Do you want to explore how two-variable equations can help us understand the world around us? If you answered yes to these questions, this article is for you! We will offer you an overview of Mathskills4kids’ solving two-variable equations worksheets designed to help 6th graders grasp detailed step-by-step methods of arriving at accurate equations.
From beginners to pros: Step-by-step instructions to master two-variable equations
Hello! If you are ready to step up your child’s math skills to the next level, grasp these step-by-step instructions prepared to help them master two-variable equations-solving skills. Whether your child struggles with equations or wants to improve their skills, this article is the perfect tool to uplift them from beginners to pros.
In this article, you will find everything you need to teach your 6th Grade students about two-variable equations, from the basics to the advanced. They will learn what they are, how to write, solve, graph, and use them in real-life situations.
You will also find links to online resources for more worksheets, games, videos, and quizzes to boost your 6th Grade learners' two-variable equations skills.
So let’s dive into the exciting world of two-variable equations!
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
-
How to identify the independent and dependent variables?
 Print it...
Print it...
-
Completing solution to 2-variable equation
 Print it...
Print it...
-
Solving linear equations in two variables word problems
 Print it...
Print it...
-
How to write two-variable linear equations
 Print it...
Print it...
-
Learn how to find the equation of a line
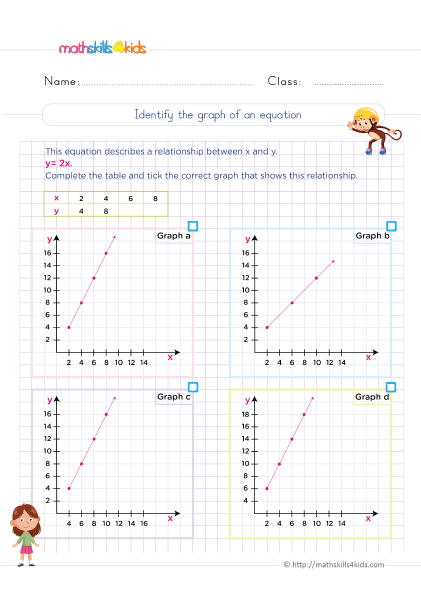 Print it...
Print it...
-
How to find an equation from a table of values
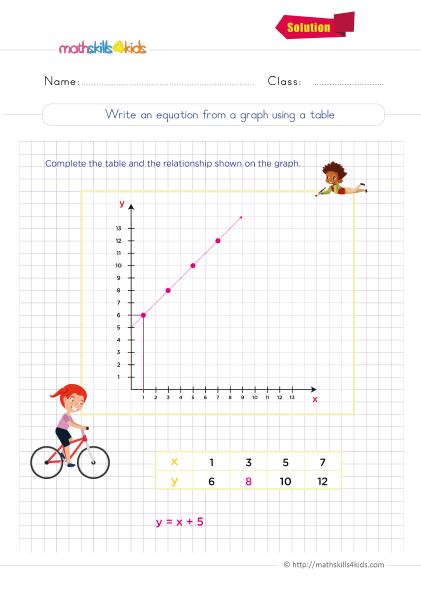 Print it...
Print it...
-
How to identify the independent and dependent variables?
-
Buying is supporting us!
Buy Now...
-
-
What are two-variable equations?
A two-variable equation is an equation that has two different variables, usually represented by letters such as x and y. For example, the equation y = 2x + 3 is a two-variable equation because it has two variables: x and y.
A variable is a symbol that can stand for any number. For example, in the equation y = 2x + 3, x can be any number, such as 0, 1, 2, -1, -2, etc. For each value of x, there is a corresponding value of y that makes the equation true. For example, if x = 0, then y = 2(0) + 3 = 3. If x = 1, then y = 2(1) + 3 = 5. If x = -1, then y = 2(-1) + 3 = 1. And so on.
Solving a two-variable equation aims to find all the possible values of x and y that make the equation true. There are different methods for doing this, which we will explore later in this article.
-
How to identify independent and dependent variables
Before we learn how to write and solve two-variable equations, we need to understand the difference between independent and dependent variables. An independent variable is a variable that can be changed or controlled by the person doing the experiment or the problem. A dependent variable is a variable that depends on the independent variable and changes as a result of it.
For example, suppose you want to find out how the height of a ball changes when you drop it from different heights. In this case, the height from which you drop the ball is the independent variable because you can control it. The height of the ball, after it bounces is the dependent variable because it depends on the independent variable and changes as a result.
In a two-variable equation, the independent variable is usually represented by x, and the dependent variable is usually represented by y. For example, in the equation, y = 2x + 3, x is the independent variable, and y is the dependent variable.
-
How to write two-variable equations from word problems
One of the most common ways to encounter two-variable equations is in word problems. A word problem is a problem that uses words and numbers to describe a situation or a question. To write a two-variable equation from a word problem, we can follow these steps:
- Read the problem carefully and identify what you are looking for and what information is given.
- Define your variables and assign them letters such as x and y.
- Write an equation that relates your variables using mathematical symbols such as +, -, x, /, =, etc.
- Check your equation by plugging in some values and seeing if it makes sense.
For example, suppose we have this word problem:
Anna has $20 more than Ben. Together they have $100. How much money does each of them have?
To write a two-variable equation from this word problem, we can follow these steps:
- Let’s read the problem carefully and identify what we are looking for and what information is given. We are looking for how much money Anna and Ben have individually. We are given that Anna has $20 more than Ben, and they have $100 together.
- Let’s define and assign variable letters such as x and y. Let x be the amount of money that Ben has, and let y be the amount that Anna has.
- We now write an equation that relates our variables using mathematical symbols such as +, -, x, /, =, Since Anna has $20 more than Ben, we can write y = x + 20. Since they have $100 together, we can write x + y = 100.
- We can now check our equation by plugging in some values and seeing if it makes sense. For example, if Ben has $10 (x = 10), then Anna has $30 (y = 10 + 20). If we add them up, we get $40, which is not equal to $100. So this is not a solution.
If Ben has $40 (x = 40), then Anna has $60 (y = 40 + 20). If we add them up, we get $100, which is equal to $100. So this is a solution.
-
How to solve two-variable equations by substitution
One of the methods for solving two-variable equations is by substitution. Substitution means replacing one variable with another expression that is equal to it. To solve two-variable equations by substitution, we need to follow these steps:
- Choose one of the equations and solve for one of the variables in terms of the other. For example, if y = 2x + 3 and x + y = 100, we can solve for y in terms of x by subtracting x from both sides: y = 100 - x.
- Substitute the expression found for the variable into the other equation and simplify. For example, if y = 2x + 3 and y = 100 - x, we can substitute 100 - x for y in the first equation and simplify: 100 - x = 2x + 3.
- Solve for the remaining variable by using inverse operations. For example, if we have 100 - x = 2x + 3, we can solve for x by subtracting 3 from both sides, adding x to both sides and dividing by 3: x = (100 - 3) / 3 = 97 / 3.
- Plug the value of the variable you found into one of the original equations and solve for the other variable. For example, if we have x = 97 / 3 and y = 2x + 3, we can plug 97 / 3 for x in the second equation and solve for y: y = 2(97 / 3) + 3 = (194 + 9) / 3 = 203 / 3.
- Check the solution by plugging the values of both variables into both original equations and seeing if they are true. For example, if we have x = 97 / 3 and y = 203 /3, we can plug them into both original equations and see if they are true:
y = 2x + 3
203 / 3 = 2(97 / 3) + 3
203 / 3 = (194 + 9) / 3
203 / 3 = 203 / 3 ✔
x + y = 100
(97 / 3) + (203 / 3) = 100
(97 + 203) / 3 = 100
300 / 3 = 100
100 = 100 ✔
Since both equations are true, the solution is correct.
-
How to solve two-variable equations by elimination
Another method for solving two-variable equations is elimination. This method involves adding or subtracting the two equations to eliminate one of the variables. Then, we can solve for the remaining variable and use it to find the value of the other variable. Let's see how this works with an example.
Example: Solve the system of equations by elimination.
x + y = 10
x - y = 2
To eliminate one of the variables, we need to make the coefficients of that variable equal in both equations. In this case, the coefficients of x are already equal, so we can eliminate x by subtracting the second equation from the first equation.
x + y = 10
(x - y = 2)
------------
0 + 2y = 8
Now we have a one-variable equation that we can solve for y.
2y = 8
y = 8/2
y = 4
We found the value of y, but we still need to find the value of x. We can do that by plugging y into either of the original equations and solving for x.
x + y = 10
x + 4 = 10
x = 10 - 4
x = 6
We found the values of both variables, so our solution is (x, y) = (6, 4).
We can check our answer by plugging these values into both equations and ensuring they are true.
6 + 4 = 10
10 = 10 ✔
6 - 4 = 2
2 = 2 ✔
Both equations are true, so our solution is correct.
-
How to graph two-variable equations on a coordinate plane
Another way to represent and solve two-variable equations is by graphing them on a coordinate plane. A coordinate plane is a grid with two axes: the x-axis (horizontal) and the y-axis (vertical). Each point on the plane has an x-coordinate and a y-coordinate that show its position on the grid.
To graph a two-variable equation, we need to find at least two points that satisfy the equation. Then, we plot those points on the coordinate plane and draw a line through them. The line represents all the possible solutions of the equation.
For example, let's graph the equation y = 2x + 3.
To find two points that satisfy this equation, we can choose any value for x and plug it into the equation to find the corresponding value for y. For example;
- If we choose x = 0, then y = 2(0) + 3 = 3. So one point is (0, 3).
- If we choose x = 1, then y = 2(1) + 3 = 5. So another point is (1, 5).
We plot these points on the coordinate plane and draw a line through them. The line shows all the pairs of x and y that make the equation true.

[Graph of y=2x+3] -
How to use two-variable equations to model real-life situations
Two-variable equations can be used to model real-life situations involving two unknown quantities related to each other. For example, suppose you want to buy some apples and bananas from a store. The apples cost $1 each, and the bananas cost $0.50 each. You have $10 to spend, and you want to buy 15 fruits. How many apples and bananas can you buy?
To answer this question, we can write two equations representing the situation. One equation relates the number of apples (x) and bananas (y) to the total number of fruits (15).
x + y = 15
The other equation relates the number of apples (x) and bananas (y) to the total cost ($10).
1x + 0.5y = 10
These two equations form a system of equations we can solve by any method we learned: substitution, elimination, or graphing. For example, using elimination, we can multiply the first equation by -0.5 and add it to the second equation to eliminate y.
-0.5(x + y = 15)
+ (1x + 0.5y = 10)
------------------------
-0.5x - 0.5y = -7.5
+ x + 0.5y = 10
------------------------
0.5x = 2.5
Then, we can solve for x and plug it into either equation to find y.
0.5x = 2.5
x = 2.5/0.5
x = 5
1x + 0.5y = 10
1(5) + 0.5y = 10
5 + 0.5y = 10
0.5y = 10 - 5
0.5y = 5
y = 5/0.5
y = 10
The solution is (x, y) = (5, 10). This means you can buy 5 apples and 10 bananas with $10.
However, this answer does not make sense in the context of the problem because you cannot buy fractions of fruits. So, we must look for another solution with whole numbers for x and y.
One way is to graph the two equations and see where they intersect on the coordinate plane.

[Graph of x+y=15 and x+0.5y=10] The graph shows that the two lines intersect at the point (5, 10). This means another solution is (x, y) = (5, 10). This means you can buy 5 apples and 10 bananas with $10. This answer makes sense in the context of the problem because it has whole numbers for x and y, and it satisfies both equations.
One possible way to buy 15 fruits with $10 is to buy 5 apples and 10 bananas.
-
How to compare and contrast different methods for solving two-variable equations
We have learned three methods for solving two-variable equations: substitution, elimination, and graphing. Each method has its advantages and disadvantages, depending on the situation. Let’s compare and contrast them:
Substitution is a method that involves solving one equation for one variable and plugging it into the other equation to eliminate that variable. This method is useful when one of the variables has a coefficient of 1 or -1 because it makes it easy to isolate that variable.
However, this method can be tedious or complicated when the coefficients are large or fractions because it involves much algebraic manipulation.
Elimination is a method that involves adding or subtracting two equations to eliminate one of the variables. This method is useful when the coefficients of one of the variables are equal or opposite in both equations because it makes it easy to eliminate that variable.
However, this method can also be tedious or complicated when the coefficients are not equal or opposite because it involves multiplying one or both equations by a factor to make them equal or opposite.
Graphing is a method that involves finding two points that satisfy each equation and drawing a line through them on a coordinate plane. This method is useful when the equations are simple or linear because it makes it easy to find and plot the points.
However, this method can be inaccurate or impossible when the equations are complex or nonlinear because it can be hard to find and plot the points or draw the curve.
Each method has pros and cons, so choosing the best method for each problem is essential based on the given equations and the situation.
-
How to challenge 6th graders with more complex two-variable equations
If you want to challenge your 6th graders with more complex two-variable equations, Mathskills4kids.com has provided some ways to do so:
- Try solving two-variable equations with fractions or decimals as coefficients or constants. For example, solve the equation system: (1/2)x + (3/4)y = 5 and (2/3)x - (4/5)y = -1.
- Try solving two-variable equations with exponents or radicals as variables or constants. For example, solve the equation system: x2 + y2 = 25 and x + y = 7.
- Try solving two-variable equations that have more than two variables. For example, solve the equation system: x + y + z = 6, x - y + z = 4, and x + y - z = 2.
- Try solving two-variable equations that have no solution or infinitely many solutions. For example, solve the equation system: x + y = 3 and 2x + 2y = 7.
- Try solving word problems that involve two-variable equations and require logical reasoning or critical thinking skills. For example, solve this problem: A school sells tickets for a play. The tickets cost $5 for adults and $3 for students. The school sold a total of 120 tickets and collected $480. How many adult tickets and how many student tickets were sold?
Bonus: Where to find more online resources to boost your 6th graders’ two-variable equations skills.
Apart from Mathskills4kids.com website, you may want to give your 6th graders more practice with two-variable equations. We will recommend you more online resources that you can use to boost your 6th graders’ two-variable equations skills. They include:
- Khan Academy: This website has video lessons, interactive exercises, and quizzes on two-variable equations and systems of equations. You can learn at your own pace and track your progress. https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:systems-of-equations.
- Math is Fun: This website has clear explanations, examples, and worksheets on two-variable equations and how to solve them by different methods. You can also play games and puzzles to test your skills. https://www.mathsisfun.com/algebra/systems-linear-equations.html.
- IXL: This website has online practice problems on two-variable equations and systems of equations for different grade levels. You can get instant feedback and hints as you solve them. https://www.ixl.com/math/grade-6/solve-a-system-of-equations-by-graphing.
- Math Games: This website has fun and engaging games that let you practice two-variable equations and systems of equations. You can choose from different topics, levels, and modes. https://www.mathgames.com/skill/6.72-solve-a-system-of-equations-using-any-method.
- Math Playground: This website has interactive activities and challenges that let you explore two-variable equations and systems of equations. You can also watch videos and animations to learn more. https://www.mathplayground.com/AlgebraEquations.html.
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
Two-variable equations are a powerful tool for modeling and solving real-life problems. They can help us understand how different variables relate to each other and how to find their values.
In this article, your students learned what two-variable equations are, how to write them from word problems, how to solve them by different methods, how to graph them on a coordinate plane, how to use them to model real-life situations, how to compare and contrast different methods for solving them, how to apply them to algebraic expressions, and how you can challenge them with more complex two-variable equations.
You also learned where to find more online resources to boost your 6th graders’ two-variable equations skills. We hope you enjoyed this article and learned something new.
Remember to practice with your kids often and have fun with math!
