6th Grade geometry worksheets: Perimeters, surface area, and volume measurements
Are you ready to help your 6th-grade students to become better problem solvers with geometry? Then, let's get started and have fun with Mathskills4kids’ 6th-grade geometry worksheets practice. Apart from finding a shape's length, area, or volume using formulas, tools, or reasoning, geometric measurement also involves finding a shape's perimeter, surface area, or volume measurements using formulas, tools, or reasoning.
-
Perimeter is the distance around a shape. Surface area is the area of the faces of a 3D shape. Volume is the space inside a 3D shape.
Geometric measurement skills can help your 6th graders become better problem solvers.
Welcome to this article on 6th-grade geometry worksheets! Geometry is the branch of mathematics that deals with shapes, sizes, angles, and positions. Geometric measurement skills are among the most important skills your 6th graders need to become better problem solvers.
Also, geometry is a very useful and fun subject to learn because it helps us better understand the world around us. We can use geometry to measure and compare different objects, to design and create new things, and to solve many kinds of problems.
This article will provide examples of common shapes and their perimeters, surface areas, and volumes. We will also provide exercises to help students apply what they have learned. Also, they will learn how to apply geometry concepts to real-life situations and other resources to help them improve their geometric measurement skill.
Let’s get started!
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
-
Finding perimeter of plane figures practice
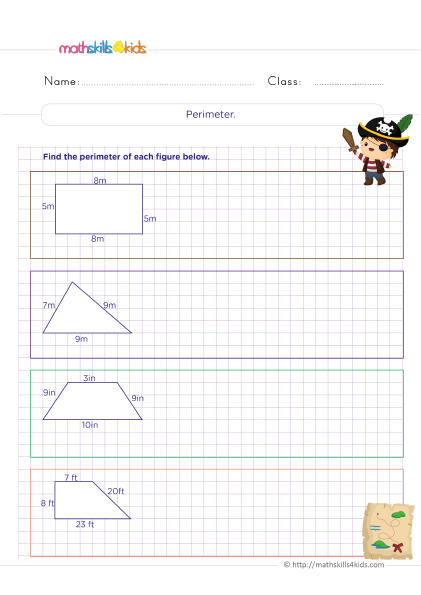 Print it...
Print it...
-
How to find area of rectangles and squares
 Print it...
Print it...
-
How do I fing area of triangles? - Geometry measurement
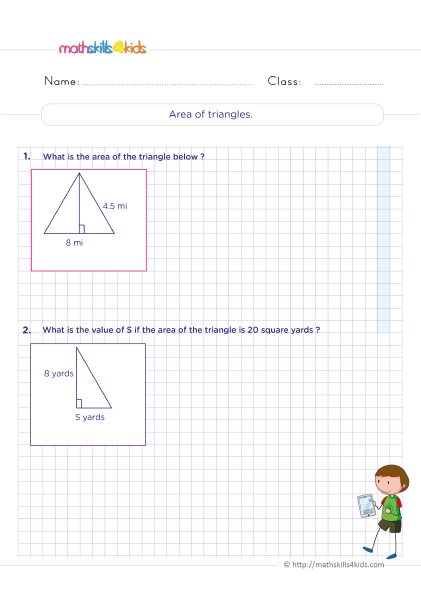 Print it...
Print it...
-
Calculate area of parallelograms and trapezoids
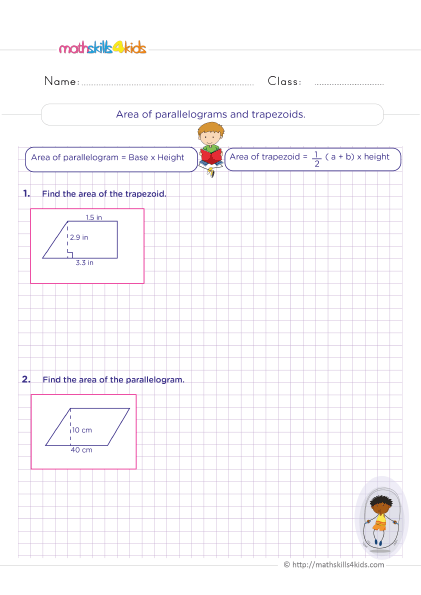 Print it...
Print it...
-
How do I find area of composite figures?
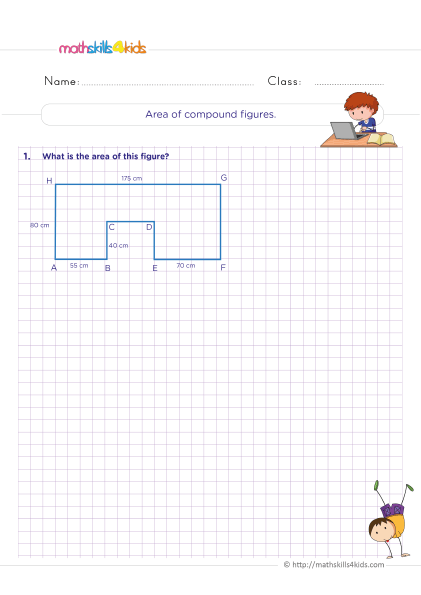 Print it...
Print it...
-
Calculate area, circumference, radius and diameter of circle
 Print it...
Print it...
-
Finding perimeter of plane figures practice
-
Buying is supporting us!
Buy Now... -
-
Volumes of cubes and rectangular prisms word problems
 Print it...
Print it...
-
Finding volume of triangular prism
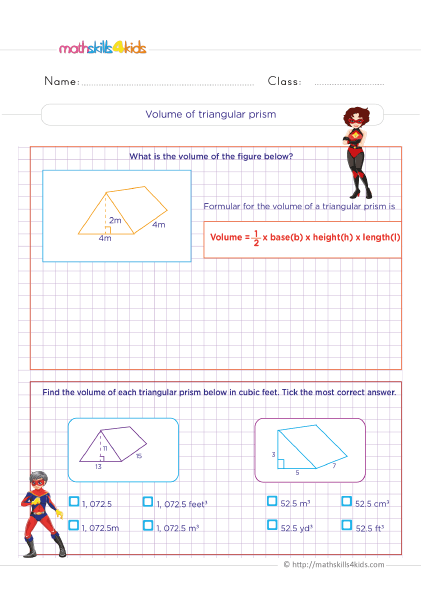 Print it...
Print it...
-
How to find surface area of pyramids
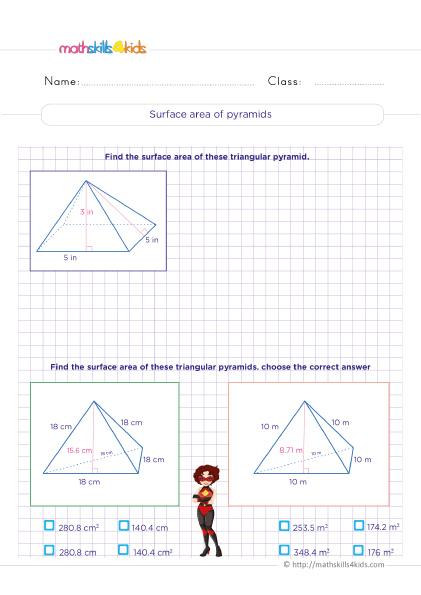 Print it...
Print it...
-
Volume and surface area of cylinders
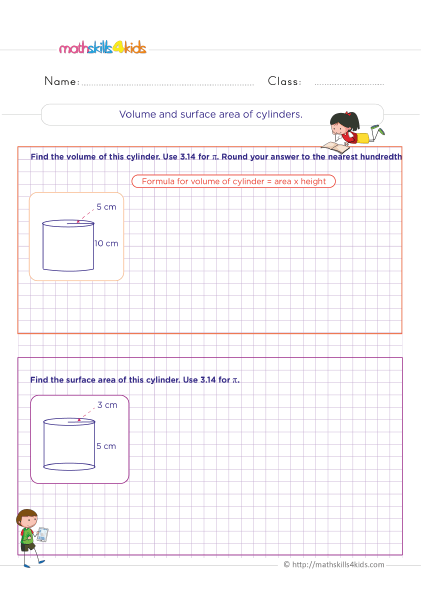 Print it...
Print it...
-
Semicircles: calculate area, perimeter, radius, nd diameter
 Print it...
Print it...
-
Area of compound figures with triangles
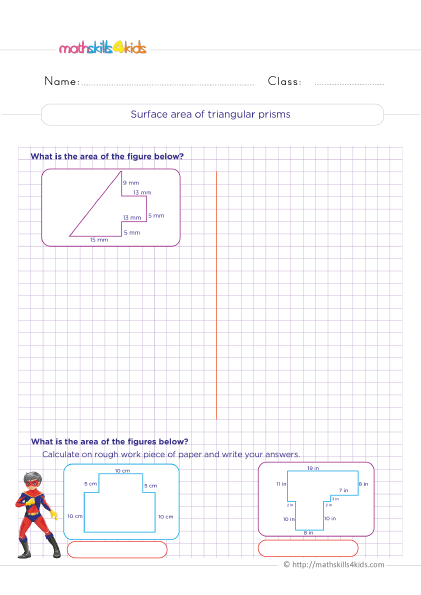 Print it...
Print it...
-
Volumes of cubes and rectangular prisms word problems
-
-
What is the importance of practicing perimeter, surface area, and volume measurements in 6th Grade?
Perimeter, surface area, and volume measurements are three important concepts in 6th-grade geometry that help students measure different aspects of shapes. Students can develop their spatial reasoning and problem-solving skills by practicing these concepts.
They will also learn how to use formulas and tools to find the measurements of various shapes. These skills can help them in many areas of math and science, such as algebra, physics, engineering, and more. They can also help students to understand the world around them better and to solve real-life problems involving shapes and space.
-
Perimeter: How to measure the distance around a shape
The perimeter of a shape is the total distance around its boundary. To find the perimeter of a shape, we need to add up the lengths of all its sides. For example, the perimeter of a square with a side length of 5 cm is 5 + 5 + 5 + 5 = 20 cm. The perimeter of a rectangle with a length of 8 cm and a width of 6 cm is 8 + 6 + 8 + 6 = 28 cm.
Some shapes have unique formulas for their perimeters. For example, the perimeter of a circle with a radius of r is 2πr, where π is approximately 3.14. The perimeter of a regular polygon with n sides and a side length of s is ns. A regular polygon is a shape that has equal sides and angles.
To measure the perimeter of a shape, we use tools such as rulers, tape measures, or string. We can also use reasoning and estimation to find the perimeter of a shape if we know some information about it. For example, if you know that a square has an area of 25 cm2, you can find its side length by taking the square root of 25, which is 5 cm. Then, you can find its perimeter by multiplying 5 by 4, which is 20 cm.
-
Surface area: How to measure the area of the faces of a 3D shape
The surface area of a 3D shape is the total area of all its faces. To find the surface area of a 3D shape, we need to add up the areas of all its faces. For example, the surface area of a cube with an edge length of 4 cm is 6 × (4 × 4) = 96 cm2. This is because a cube has six faces that are all squares with an area of 4 × 4 cm2.
Some 3D shapes have unique formulas for their surface areas. For example, the surface area of a sphere with a radius of r is 4πr2. The surface area of a cylinder with a radius of r and a height of h is 2πr2 + 2πrh. The surface area of a cone with a radius of r and a slant height of l is πr2 + πrl.
To measure the surface area of a 3D shape, we can use tools such as rulers, protractors, or nets. A net is a flat pattern that can be folded to make a 3D shape. We can also use reasoning and estimation to find the surface area of a 3D shape if we know some information about it.
For example, if you know that a cube has a volume of 64 cm3, you can find its edge length by taking the cube root of 64, which is 4 cm. Then you can find its surface area by multiplying 6 by (4 × 4), which is 96 cm2.
-
Volume: How to measure the space inside a 3D shape
Another important concept in geometry is volume. Volume is the amount of space that a 3D shape occupies. We can think of volume as how much water a shape can hold or how many cubes can fit inside a shape.
To find the volume of a 3D shape, we need to know its base area and height. The base area is the area of the face that the shape stands on. The height is the distance from the base to the opposite face. The formula for volume is:
Volume = Base area x Height
For example, to find the volume of a rectangular prism, multiply the area of the rectangular base by the height of the prism. The area of a rectangle is length x width, so the formula for volume is:
Volume = Length x Width x Height
Some 3D shapes have different formulas for volume, depending on their shape. For example, to find the volume of a cylinder, multiply the circular base's area by the cylinder's height. The area of a circle is pi x radius squared, so the formula for volume is:
Volume = Pi x Radius squared x Height
Here are some other common 3D shapes and their formulas for volume:
- Cube: Volume = Side cubed
- Sphere: Volume = 4/3 x Pi x Radius cubed
- Cone: Volume = 1/3 x Pi x Radius squared x Height
- Pyramid: Volume = 1/3 x Base area x Height
-
Examples: Some common shapes and their perimeters, surface areas, and volumes
To help your 6th graders understand these concepts better, let's look at some examples of common shapes and their measurements, i.e., perimeters, surface areas, and volumes. Students can use these examples as a reference when practicing their calculations.
- Rectangle: A rectangle is a 2D shape with four sides and four right angles. The opposite sides are equal and parallel.
Perimeter = 2 x Length + 2 x Width
Surface area = Length x Width
Volume = Length x Width x Height
For example, if a rectangle has a length of 10 cm, a width of 5 cm, and a height of 3 cm, then:
Perimeter = 2 x 10 + 2 x 5 = 30 cm
Surface area = 10 x 5 = 50 cm squared
Volume = 10 x 5 x 3 = 150 cm cubed
- Circle: A circle is a 2D shape with no sides or angles. It has a center point and a radius, the distance from the center to any point on the circle.
Perimeter (also called circumference) = 2 x Pi x Radius
Surface area (also called area) = Pi x Radius squared
Volume (of a sphere) = 4/3 x Pi x Radius cubed
For example, if a circle has a radius of 4 cm, then:
Perimeter = 2 x Pi x 4 = 25.13 cm (approx.)
Surface area = Pi x 4 squared = 50.27 cm squared (approx.)
Volume (of a sphere) = 4/3 x Pi x 4 cubed = 268.08 cm cubed (approx.)
- Triangle: A triangle is a 2D shape with three sides and three angles. The sum of the angles in any triangle is always 180 degrees.
Perimeter = Side A + Side B + Side C
Surface area (also called area) = Base x Height / 2
Volume (of a pyramid) = Base area x Height / 3
For example, if a triangle has a base of 6 cm, a height of 4 cm, and sides of length 5 cm, then:
Perimeter = 5 + 5 + 6 = 16 cm
Surface area = 6 x 4 / 2 = 12 cm squared
Volume (of a pyramid) = Base area x Height /3
= (6x4/2) x (4/3)
=12 x (4/3)
=16 cm cubed
- Rectangle: A rectangle is a 2D shape with four sides and four right angles. The opposite sides are equal and parallel.
-
Practice: Some exercises for 6th graders to apply what they learned
Now that your 6th graders have learned about perimeters, surface areas, and volumes, it's time to practice their skills. Here are some exercises from Mathskills4kids’ 6th-grade geometry worksheets that they can try to solve independently. They can use rulers, protractors, or calculators to measure shapes. They can also use reasoning and estimation to check their answers.
Find the perimeter, surface area, and volume of each shape below. Round your answers to two decimal places if necessary.
- A square with a side length of 8 cm.
- A circle with a radius of 5 cm.
- A cube with an edge length of 6 cm.
- A cylinder with a radius of 3 cm and height of 10 cm.
- A cone with a radius of 4 cm and height of 12 cm.
Find the missing measurements of each shape below. Round your answers to two decimal places if necessary.
- A rectangle with a length of 15 cm and a perimeter of 46 cm. What is the width and the surface area?
- A circle with an area of 78.54 cm squared. What is the radius and the perimeter?
- A sphere with a volume of 523.6 cm cubed. What is the radius and the surface area?
- A pyramid with a base area of 36 cm squared and a volume of 48 cm cubed. What is the height and the surface area?
- A triangular prism with a base area of 18 cm squared, height of 9 cm, and volume of 162 cm cubed. What is the length and the surface area?
-
How to apply geometry concepts to real-life situations
Geometry is useful in the math class and also in everyday life. We can use geometric measurement concepts to solve real-life situations such as:
- How much paint do you need to cover a wall or a room?
- How much wrapping paper do you need to wrap a gift box?
- How much water can a tank or a bottle hold?
- How much space do you need to store or pack some items?
- How much land do you own or need to buy?
- How much fence do you need to enclose a garden or a yard?
To solve these problems, we need to identify the shapes involved and their dimensions. Then, use the appropriate formulas to find the measurements that are needed. We also need to pay attention to the units of measurement and convert them if necessary.
Here are some more examples of how to apply geometry concepts to real-life situations:
- If you want to paint a wall, you need to know its surface area to buy enough paint. You can use the formula for the surface area of a rectangle to find the answer.
- If you want to buy a new backpack, you need to know its volume to see how much stuff you can fit inside. You can use the formula for the volume of a prism to find the answer.
- If you want to make a fence around your garden, you need to know its perimeter to buy enough wood. You can use the formula for the perimeter of a polygon to find the answer.
- If you want to design a logo, you need to know how to use angles and shapes to create a symmetrical and appealing image. You can use protractors and rulers to measure angles and shapes.
- To plan a trip, know how to use maps and scales to estimate distances and time. You can use ratios and proportions to convert measurements.
As you can see, geometry is everywhere and can help us with many things. The more your students practice geometric measurement skills, the more confident and creative they will become.
Bonus: What other resources can help 6th graders to practice their geometric measurement skills?
If you want your 6th graders to learn more about geometry and practice their geometric measurement skills, many resources can help you. Here are some web links with descriptions that you can check out:
- https://www.mathsisfun.com/geometry/index.html: This website has interactive lessons, games, quizzes, and worksheets on various geometry topics, such as angles, shapes, area, volume, and more.
- https://www.khanacademy.org/math/cc-sixth-grade-math/cc-6th-geometry-topic: This website has videos, articles, and exercises on 6th-grade geometry topics, such as area and perimeter, surface area and volume, angles, and coordinate plane.
- https://www.mathplayground.com/index_geometry.html: This website has fun and challenging games that test students’ geometry skills, such as finding missing angles, calculating area and perimeter, matching shapes, and more.
- https://www.mathworksheets4kids.com/geometry.php: This website has printable worksheets that cover various geometry topics, such as polygons, circles, triangles, quadrilaterals, transformations, symmetry, and more.
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
In this article, you and your 6th-grade students have learned more about perimeter, surface area, and volume measurements. 6th graders have learned what they are and why they are important. They have learned how to calculate them using formulas, how to use tools such as rulers, protractors, or calculators to measure shapes, how to use reasoning and estimation to find measurements, how to apply geometric measurement concepts to real-life problems, and how to find more resources to practice their geometric measurement skill.
We hope this article helped your students become better problem solvers with geometry. Remember that geometry is not only useful for math class but also for everyday life. The more kids practice their geometric measurement skills, the more confident and creative they will become.
Thank you for reading this article. We hope you enjoyed it and learned something new. Have fun with geometry!
