6th-grade basics equations worksheet: One-Step, One-Variable, and Linear Equations
Hello, and welcome to the world of equations! Mathskills4kids.com is a fantastic website with a remarkable collection of 6th-grade basic equations worksheets that will help your 6th Grade students master one-step, one-variable, and linear equations in no time!
-
In this article, 6th graders will learn these types of equations, why they are essential, and how to easily solve them. They will also discover tips and tricks for tackling 6th-grade math problems and fun ways to practice their skills. Also, by the end of this article, they will be ready to ace their 6th-grade math tests and impress their friends and teachers with fantastic equation-solving abilities!
6th Grade math made simple: A step-by-step approach to one-step, one-variable, and linear equations
Math can be intimidating for many students, especially when encountering new concepts and symbols that seem complicated and confusing. But don't worry! This article aims to make 6th Grade math simple and fun. An example is seen with our step-by-step approach for solving one-step, one-variable, and linear equations, one of the vital skills students need to succeed in 6th-grade math.
Equations are mathematical statements that show the relationship between two or more quantities. For example, 2 + 3 = 5 is an equation that shows that adding 2 and 3 gives the same result as 5. Solving equations means finding the value or values that make the equation true. For example, x + 3 = 5 is an equation that can be solved by finding the value of x that makes it true. In this case, x = 2, because 2 + 3 = 5.
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
-
Solving one-step equations
exercises Print it...
Print it...
-
Writing one-step equations from word problems
 Print it...
Print it...
-
Modelling and solving equation using algebra tiles
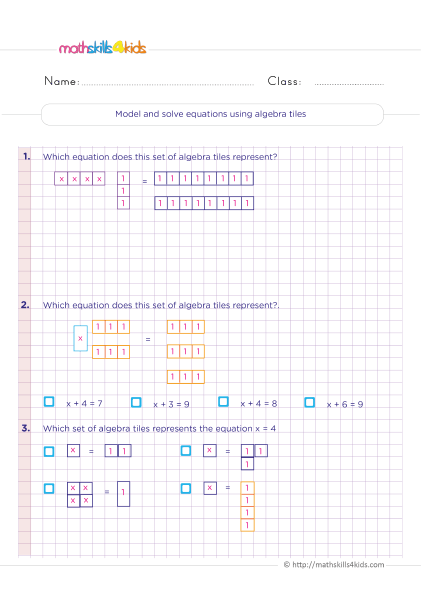 Print it...
Print it...
-
One-step addition and subtraction equations
 Print it...
Print it...
-
Solving one-step equation with whole numbers
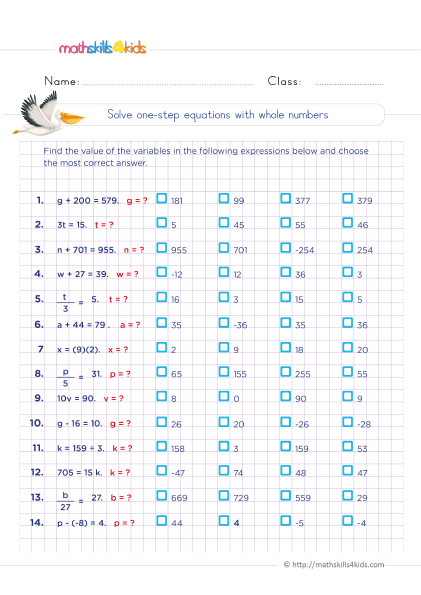 Print it...
Print it...
-
How to solve equations involving like terms
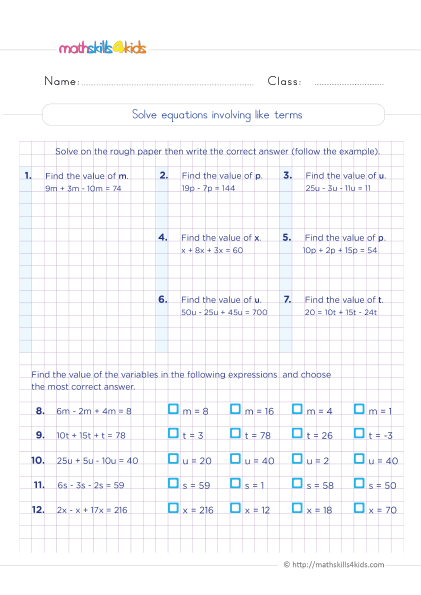 Print it...
Print it...
-
Solving one-step equations
-
Buying is supporting us!
Buy Now...
-
-
Definition: What are one-step, one-variable, and linear equations, and how to recognize them
There are many types of equations that your students will encounter in math, but in this article, we will focus on three basic ones: one-step, one-variable, and linear equations. These are the simplest and most common types of equations that students will need to solve in 6th-grade math. Here is how to recognize them:
- One-step equations can be solved in one step by performing one operation (such as addition, subtraction, multiplication, or division) on both sides of the equation. For example, x + 5 = 10 is a one-step equation that can be solved by subtracting 5 from both sides:
x + 5 - 5 = 10 - 5, which simplifies to x = 5.
- One-variable equations have only one unknown quantity, usually represented by a letter such as x or y. For example, x + 5 = 10 is a one-variable equation because it has only one unknown quantity, x. Depending on their complexity, one-variable equations can have more than one step to solve. For example, 2x - 3 = 7 is a one-variable equation requiring two steps: First, add 3 to both sides, then divide both sides by 2.
- Linear equations have two variables (usually x and y) and form a straight line when graphed on a coordinate plane. For example, y = 2x + 3 is a linear equation because it has two variables, y, and x, and it forms a straight line with a slope of 2 and a y-intercept of 3 when graphed.
Linear equations can also be written in other forms, such as Ax + By = C or y - y1 = m(x - x1), where A, B, C, m, x1, and y1 are constants.
- One-step equations can be solved in one step by performing one operation (such as addition, subtraction, multiplication, or division) on both sides of the equation. For example, x + 5 = 10 is a one-step equation that can be solved by subtracting 5 from both sides:
-
Why 6th Grade math matters: How learning one-step, one-variable, and linear equations can boost 6th graders’ confidence and skills
Do you know why 6th Grade math matters? You might wonder how learning one-step, one-variable, and linear equations can boost 6th graders’ confidence and skills. What's the point of finding the value of x or y if you already know the answer?
Well, there are many reasons why learning how to solve equations is essential and beneficial for your student’s math education and beyond. Here are some of them:
- Solving equations helps students develop logical thinking and problem-solving skills. When solving an equation, apply the rules of arithmetic and algebra systematically and consistently.
Also, follow a particular order of operations and use inverse operations to undo what has been done to the unknown quantity.
You can also check your answer by plugging it back into the original equation and ensuring it works. These skills are essential for solving more complex math problems later on and other subjects such as science and engineering.
- Solving equations helps students understand the meaning and structure of mathematical expressions. When solving an equation, interpret each symbol and term's meaning and how they relate.
You must understand what an equation represents and what it asks you to find. You also have to understand how different forms of equations convey different information about the relationship between the variables.
These skills help us communicate effectively using mathematical language and notation.
- Solving equations helps learners explore and discover patterns and relationships in math. When solving an equation, you often find multiple ways to get to the same answer or different types of solutions depending on the equation.
You also find connections and similarities between different types of equations and how they can be transformed or manipulated.
These skills help us appreciate the beauty and elegance of math and how it can be used to model and explain real-world phenomena.
- Solving equations helps students develop logical thinking and problem-solving skills. When solving an equation, apply the rules of arithmetic and algebra systematically and consistently.
-
The basics of one-step equations: How to solve them using addition, subtraction, multiplication, and division
Now that your 6th graders know what one-step equations are and why they are essential, let's learn how to solve them using the four basic operations: addition, subtraction, multiplication, and division. The general rule for solving one-step equations is to use the inverse operation of what has been done to the unknown quantity and perform the same operation on both sides of the equation.
For example, if x has been added by 5, subtract 5 from both sides to isolate x.
Here are some examples of how to solve one-step equations using each operation:
- Addition: If x has been added by a number, then subtract that number from both sides. For example, to solve x + 7 = 12, subtract 7 from both sides: x + 7 - 7 = 12 - 7, which simplifies to x = 5.
- Subtraction: If x has been subtracted by a number, then add that number to both sides. For example, to solve x - 4 = 9, add 4 to both sides: x - 4 + 4 = 9 + 4, which simplifies to x = 13.
- Multiplication: If x has been multiplied by a number, then divide both sides by that number. For example, to solve 3x = 15, divide both sides by 3: 3x / 3 = 15 / 3, which simplifies to x = 5.
- Division: If x has been divided by a number, then multiply both sides by that number. For example, to solve x / 2 = 6, multiply both sides by 2: x / 2 x 2 = 6 x 2, which simplifies to x = 12.
Your students must remember to always check their answer by plugging it back into the original equation and making sure it works. For example, if we found that x = 5 for the equation x + 7 = 12, then we must plug in x = 5 and see if it makes the equation true: (5) + 7 = 12, which is true.
-
The basics of one-variable equations: How to find the value of an unknown number using algebraic expressions
One-variable equations have only one unknown number, usually represented by a letter like x, y, or z. For example, x + 5 = 10 is a one-variable equation because it has only one unknown number, x. To find the value of x, we need to use algebraic expressions, which are combinations of numbers, variables, and operations like addition, subtraction, multiplication, and division.
The main idea of solving one-variable equations is to isolate the variable on one side of the equation and the numbers on the other. To do this, we need to use the opposite operation of what is given in the equation. For example, if x + 5 = 10, we will subtract 5 from both sides of the equation to get x = 5. This means that x equals 5, and we have solved the equation.
Here are some more examples of how to solve one-variable equations using algebraic expressions:
- y - 3 = 7: To isolate y, we add 3 to both sides of the equation. This gives us y = 10.
- z x 4 = 12: To isolate z, we divide both sides of the equation by 4. This gives us z = 3.
- w / 2 = 6: To isolate w, we multiply both sides of the equation by 2. This gives us w = 12.
We can use these steps to solve any one-variable equation using algebraic expressions. But we must remember to do the same thing to both sides of the equation and use the opposite operation of what is given.
-
The basics of linear equations: How to graph them using slope and intercept
Linear equations make a straight line when we graph them on a coordinate plane. A coordinate plane is a grid with two axes: the x-axis (horizontal) and the y-axis (vertical). Each point on the coordinate plane has an x-coordinate (the horizontal distance from the origin) and a y-coordinate (the vertical distance from the origin). For example, point (2, 3) has an x-coordinate of 2 and a y-coordinate of 3.
To graph a linear equation, we need to know the slope and the intercept. The slope measures how steep the line is and tells us how much the y-coordinate changes when the x-coordinate changes by one unit. The intercept is a point where the line crosses either the x-axis or the y-axis.
The most common form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept. For example, y = 2x + 5 is a linear equation with a slope of 2 and a y-intercept of 5. To graph this equation, we can follow these steps:
- Start at the y-intercept, which is (0, 5) in this case.
- Use the slope to find another point on the line. Since the slope is 2, there is a two-unit increase in y for every one-unit increase in x. So, if we move one unit to the right from (0, 5), we get (1, 7). This is another point on the line.
- Draw a straight line through these two points. This is the graph of y = 2x + 5.
Here are some more examples of how to graph linear equations using slope and intercept:
- y = -x + 3: This equation has a slope of -1 and a y-intercept of 3. To graph it, we start at (0, 3) and use the slope to find another point on the line. Since the slope is -1, this means that for every one-unit increase in x, there is a one-unit decrease in y. So, if we move one unit to the right from (0, 3), we get (1, 2). This is another point on the line. We draw a straight line through these two points.
- y = x - 2: This equation has a slope of 1 and a y-intercept of -2. To graph it, we start at (0, -2) and use the slope to find another point on the line. Since the slope is 1, there is a one-unit increase in x for every one-unit increase in y. So, if we move one unit to the right from (0,-2), we get (1,-1). This is another point on the line. We draw a straight line through these two points.
We can use these steps to graph any linear equation using slope and intercept. Remember to find the y-intercept and use the slope to find another point on the line.
-
Tips and tricks for solving 6th-grade math problems: How to check your answers, avoid common mistakes, and use helpful resources
Solving 6th-grade math problems can be fun, rewarding but also challenging and frustrating. Here are some tips and tricks to help your students succeed in 6th-grade math:
- Check answers: After solving a problem, students should always check their answer to make sure it makes sense and is correct. They can check their answer by plugging it back into the equation, using a different method, or using a calculator.
For example, if you solved x + 5 = 10 and got x = 5, you can check your answer by plugging it back into the equation: 5 + 5 = 10. This is true, so your answer is correct.
You can also check your answer using a different method, such as subtracting 5 from both sides of the equation: x + 5 - 5 = 10 - 5, which gives x = 5. This is the same answer, so your answer is correct.
You can also check your answer using a calculator: if you type in x + 5 = 10 and press solve, you will get x = 5. This is the same answer, so your answer is correct.
- Avoid common mistakes: When solving math problems, students should be careful to avoid common mistakes that can lead to wrong answers. Some common mistakes are:
- Forgetting to do the same thing to both sides of the equation: When solving equations, always do the same thing to both sides of the equation to keep it balanced.
For example, if you have x + 5 = 10 and want to subtract 5 from both sides, write x + 5 -5 = 10 - 5, not x = 10 - 5.
- Mixing up the order of operations: When performing operations on numbers or expressions, follow the order of operations, which is parentheses, exponents, multiplication and division (from left to right), and addition and subtraction (from left to right).
For example, if you have 2 + (3 x 4) - 5, multiply inside the parentheses first: 2 + (12) - 5. Then add and subtract from left to right: 14 - 5. The final answer is 9.
- Confusing positive and negative signs: When working with positive and negative numbers, follow the rules for adding, subtracting, multiplying, and dividing them carefully.
For example, when adding two numbers with the same sign, add their absolute values (the distance from zero) and keep their sign. When adding two numbers with different signs, subtract their absolute values and take the sign of the larger number. When multiplying or dividing two numbers with the same sign, the result is positive. When multiplying or dividing two numbers with different signs, the result is negative.
- Use helpful resources: If students are stuck on a problem or need more practice, they can use helpful resources to help them learn and improve their skills. Some helpful resources are:
- The teacher: The teacher is the best resource for learning math. Students can ask their teacher questions during or after class or email them with any doubts or concerns.
The teacher can explain concepts, give examples, provide feedback, and offer guidance.
- Textbook: The textbook is another excellent resource for learning math. Students can read their textbook carefully to understand the concepts, review the examples, do the exercises, and check their answers with the answer key.
- Online tools: Many online tools can help students with math. They can use online calculators to check their answers or perform calculations. They can use online videos to watch explanations or demonstrations of math concepts. They can use online games to practice their skills in a fun way. They can use online quizzes to test their knowledge or prepare for exams.
- Check answers: After solving a problem, students should always check their answer to make sure it makes sense and is correct. They can check their answer by plugging it back into the equation, using a different method, or using a calculator.
-
How to have fun with 6th Grade math: How to apply knowledge to real-life situations, games, and puzzles
One of the best ways to learn and enjoy 6th-grade math is to apply knowledge to real-life situations, games, and puzzles. This way, 6th graders can see how math is practical, fun, and creative.
Here are some examples of how students can have fun with 6th-grade math:
- Real-life situations: Your 6th graders can use one-step, one-variable, and linear equations to solve problems they encounter daily. For example, they can use one-step equations to calculate how much money they need to buy something, how much change they will get, or how much time they have left for an activity. They can use one-variable equations to determine how many items they can buy with a certain amount of money or how many people can share a pizza. They can use linear equations to model relationships between two quantities, such as the distance and time of a trip or the height and age of a person.
- Games: Students can play games that involve one-step, one-variable, and linear equations. For example, they can play tic-tac-toe with algebraic expressions, where each square has an expression, and they have to find the variable's value to place their mark.
They can also play bingo with equations, where each card has an equation, and they have to solve it to mark the number. They can also play hangman with equations, where an expression replaces each letter, and they have to guess the word by solving the equations.
- Puzzles: Students can solve puzzles challenging their 6th-grade math skills. For example, they can solve crossword puzzles with equations, where each clue is an equation, and have to find the word that matches the solution.
They can also solve logic puzzles with equations, using clues and equations to find out information about a situation. They can also solve riddles with equations, using their creativity and math knowledge to find the answer.
Bonus: Where to find more resources to reinforce basics equations solving skills for 6th Graders
Having made it to the end of this article, your 6th graders must have learned a lot about one-step, one-variable, and linear equations and how to solve them confidently and efficiently. But don't stop here! There are many more resources that you can use to help them practice and reinforce their 6th-grade equation-solving skills. Here are some of the best ones that we recommend:
- Khan Academy: This is a free online platform that offers video lessons, exercises, quizzes, and tests on various math topics, including equations. Students can watch the videos at their own pace and track their progress and achievements. Khan Academy is a great way to review what they've learned in class or learn something new independently. https://www.khanacademy.org/math/cc-sixth-grade-math
- Math Playground: This is a fun website with hundreds of games and puzzles involving math concepts, including equations. 6th graders can play games that challenge their logic, strategy, and problem-solving skills or create their puzzles and share them with others. Math Playground is a great way to have fun with math and apply their knowledge to real-life situations. https://www.mathplayground.com/
- Math Is Fun: This is another website that makes math enjoyable and easy to understand. It has explanations, examples, worksheets, and quizzes on various math topics, including equations. Students can also find interactive tools like calculators, graph makers, and equation solvers to help with homework or projects.
Math Is Fun is a great way to learn math simply and clearly. https://www.mathsisfun.com/
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
Congratulations! Your 6th graders have learned a lot about one-step, one-variable, and linear equations in 6th-grade math. They have also learned how to have fun with them by applying their knowledge to real-life situations, games, and puzzles. They should be proud of themselves for achieving this milestone in their math journey.
But they shouldn’t stop here! There is so much more to learn and explore in math. As they move on to the next level, they will encounter more complex and exciting equations that will challenge their mind and expand their horizons. They will also discover new connections between math and other subjects, such as science, art, music, and history.
So encourage your 6th-grade math learners to keep practicing their 6th-grade math skills and having fun with them. And remember: with Mathskills4kids.com, math is not complicated; it's just a matter of learning step by step!
