Learn and practice rational numbers: Grade 6 printable worksheets
Whether you're a parent or teacher looking for ways to strengthen your 6th graders' understanding of rational numbers, you’ve made an excellent choice. This article will offer the best Grade 6 printable worksheets designed by Mathskills4kids.com experts, perfect for introducing, learning, and practicing rational numbers engagingly and interactively.
-
Taking math to the next level with our Grade 6 worksheets for practicing rational numbers
Hello, take your 6th grader’s math learning to the next level with our Grade 6 worksheets for practicing rational numbers. These worksheets are designed by experienced educators and tailored to meet the needs of young learners, providing them with a solid foundation in rational numbers.
Also, these printable worksheets offer a comprehensive range of exercises and activities, from identifying rational numbers to comparing and ordering them, including essential skills needed to master this fundamental mathematical concept.
With clear instructions, colorful visuals, and various question types, our worksheets make learning rational numbers a breeze. Get started today and watch your students' understanding and confidence soar!
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
Buying is supporting us!
Buy Now...
-
-
What are rational numbers, and why are they important for 6th-graders?
What are rational numbers? These numbers can be written as fractions, where the numerator and denominator are integers. For example, 3/4, -5/2, and 0.6 are all rational numbers.
Rational numbers are important for 6th-graders because they help them understand the relationships between different types of numbers, such as fractions, decimals, and percentages. They also help them develop skills in comparing, ordering, adding, subtracting, multiplying, and dividing numbers with different forms and signs.
-
How to represent rational numbers using fractions, decimals, and percentages
Rational numbers can be represented differently using fractions, decimals, and percentages. We can use equivalent forms or common factors to convert a rational number from one form to another. For example:
- To convert 3/4 to a decimal, we can divide the numerator by the denominator: 3 ÷ 4 = 0.75.
- To convert 0.75 to a percentage, we can multiply by 100: 0.75 × 100 = 75%.
- To convert 75% to a fraction, we can write the percentage as a fraction over 100 and simplify: 75/100 = 3/4.
-
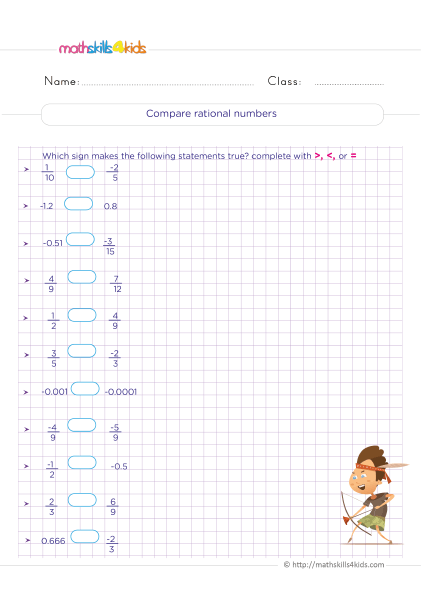
How to compare and order rational numbers using number lines and equivalent forms
We can use number lines or equivalent forms to compare and order rational numbers. A number line is a line that shows the position of numbers on a scale. We can plot rational numbers on a number line by finding their fractions or decimals equivalents. For example;
To plot -1/2 on a number line, we can convert it to a decimal: -1/2 = -0.5. Then we can find the point halfway between 0 and -1 on the number line.
To compare two rational numbers on a number line, we can see which one is closer to the right or the left. For example, -1/2 is closer to the left than 3/4, so -1/2 < 3/4.
To order rational numbers on a number line, we can arrange them from left to right in increasing order or from right to left in decreasing order.
Another way to compare and order rational numbers is to use equivalent forms. We can convert rational numbers to fractions with the same denominator or decimals with the same number of decimal places. Then we can compare or order them by looking at their numerators or decimal digits. For example:
To compare -1/2 and 3/4, we can convert them to fractions with the same denominator: -1/2 = -2/4 and 3/4 = 3/4. Then we can compare their numerators: -2 < 3, so -1/2 < 3/4.
To order -1/2 and 3/4, we can arrange them from smallest to largest or from largest to smallest: -1/2 < 3/4 or 3/4 > -1/2.
-
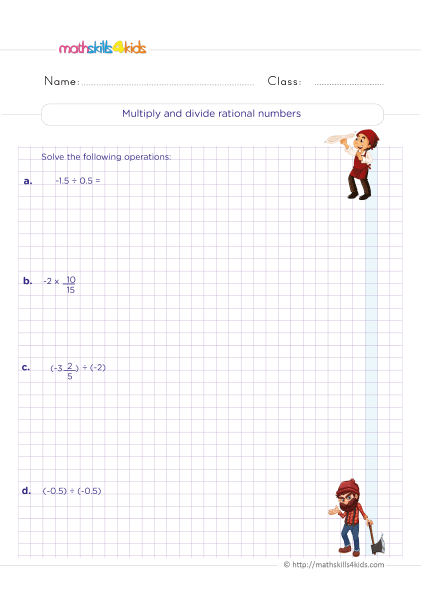
How to perform arithmetic operations with rational numbers using rules and properties
One of the most important skills 6th-graders need to master is performing arithmetic operations with rational numbers. Rational numbers can be written as fractions, decimals, or percentages. For example, 1/2, 0.5, and 50% are all rational numbers representing the same value.
To add, subtract, multiply, and divide rational numbers, we must follow some rules and properties that help us simplify the calculations and get the correct answer. Here are some of the most common rules and properties that you need to know:
- To add or subtract rational numbers with the same denominator, we add or subtract the numerators and keep the same denominator. For example, 2/5 + 3/5 = (2 + 3)/5 = 5/5 = 1.
- To add or subtract rational numbers with different denominators, we need to find a common denominator by multiplying the denominators of both numbers. Then we multiply the numerators by the same factor we used to multiply the denominators. For example, 1/4 + 2/3 = (1 x 3)/(4 x 3) + (2 x 4)/(3 x 4) = 3/12 + 8/12 = (3 + 8)/12 = 11/12.
- To multiply two rational numbers, we multiply the numerators and the denominators. For example, 2/3 x 4/5 = (2 x 4)/(3 x 5) = 8/15.
- To divide two rational numbers, we flip the second number and multiply it by the first number. This is called finding the reciprocal of a fraction. For example, 2/3 ÷ 4/5 = 2/3 x 5/4 = (2 x 5)/(3 x 4) = 10/12.
- To convert a fraction to a decimal, we divide the numerator by the denominator. For example, 3/4 = 3 ÷ 4 = 0.75.
- To convert a decimal to a fraction, we write it (the decimal) as a fraction over a power of ten and then simplify it. For example, 0.6 = 6/10 = 3/5.
- To convert a fraction to a percentage, we multiply the fraction by 100 and add a percent sign. For example, 1/4 = (1/4) x 100% = 25%.
- To convert a percentage to a fraction, we write it (the percentage) as a fraction over 100 and then simplify it. For example, 60% = 60/100 = 3/5.
These rules and properties will help your students to perform arithmetic operations with rational numbers more efficiently and accurately.
-
How to solve real-world problems involving rational numbers using strategies and models
Another vital skill students need to develop is solving real-world problems involving rational numbers using strategies and models. Rational numbers are often used to describe situations that involve fractions, decimals, or percentages of a whole or a part. For example;
You may encounter problems that ask you to find the fraction of a pizza left after eating some slices, the percentage of students who passed a test, or the decimal amount of money you need to pay for a purchase.
To solve these problems, teachers should use strategies and models to help students understand the problem, find the relevant information, choose the appropriate operation, and check their answers. Here are some of the most common strategies and models that you can use:
- Draw a picture or a diagram that represents the problem situation. For example, you can use a circle or a rectangle to represent a whole or a part of something and shade or label the fractions, decimals, or percentages given or asked for.
- Use a number line to compare and order rational numbers or to find missing values. For example, you can use a number line to show students how fractions, decimals, and percentages are equivalent or how they can be added or subtracted.
- Use manipulatives or concrete objects to model fractions, decimals, or percentages. For example, you can use fraction strips, base ten blocks, coins, or counters to show students how rational numbers can be composed or decomposed into smaller units or how they can be multiplied or divided.
- Use tables or charts to organize data or information related to rational numbers. For example, you can use tables or charts to show how fractions, decimals, or percentages can be converted from one form to another or how they can be used to calculate ratios, rates, or proportions.
- Use formulas or rules to calculate rational numbers. For example, you can use formulas or rules to find equivalent fractions, decimals, or percentages for students to perform arithmetic operations with rational numbers efficiently.
These strategies and models will help 6th graders to solve real-world problems involving rational numbers more effectively and efficiently. They can learn and practice these rational numbers using Mathskills4kids’ Grade 6 printable worksheets with different types of problems.
-
Real-world applications of rational numbers
Rational numbers are useful for solving math problems and applying concepts in various fields and disciplines. Rational numbers are often used to describe and measure quantities, relationships, patterns, and changes in the real world. For example, some real-world applications of rational numbers include:
- Comparing and contrasting different objects or phenomena using fractions, decimals, or percentages. For example, we can compare different objects' sizes, shapes, colors, or weights using fractions, decimals, or percentages.
- Expressing and interpreting data or information using fractions, decimals, or percentages. For example, we can express the results of a survey, an experiment, or a test using fractions, decimals, or percentages or interpret graphs, charts, or tables that use rational numbers to display data or information.
- Make predictions or estimations using fractions, decimals, or percentages. For example, we can make predictions or estimations about the weather, the population, the economy, or the environment using fractions, decimals, or percentages.
- Make decisions or choices using fractions, decimals, or percentages. For example, we can make decisions or choices about our budget, diet, health, or education using fractions, decimals, or percentages.
Bonus: additional resources for learning and practicing rational numbers
If you want to help your students learn more about rational numbers and practice them further, you can check out these web links that provide additional resources for learning and practicing rational numbers. These web links include:
- Khan Academy: This website offers free online lessons and exercises on various math topics, including rational numbers. You can watch videos that explain the concepts and examples of rational numbers and practice them with your students using interactive quizzes and games. You can also track their progress while they earn badges and points as they learn. You can access the website here: https://www.khanacademy.org/math/6th-grade-illustrative-math/unit-7-rational-numbers.
- Math is Fun: This website offers free online tutorials and activities on various math topics, including rational numbers. You can read articles explaining rational numbers' definitions and properties and practice them using worksheets and puzzles with your students. You can also encourage them to play games and quizzes that test their knowledge and skills on rational numbers. You can access the website here: https://www.mathsisfun.com/rational-numbers.html.
- IXL: This website offers personalized online learning and practice on various math topics, including rational numbers. You can choose from hundreds of skills that cover different aspects and levels of rational numbers and practice them with your 6th graders using interactive questions and feedback.
You can also monitor their performance and achievements as they learn. You can access the website here: https://www.ixl.com/math/grade-6/rational-numbers.
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
This article has taught us much about rational numbers and why they are essential for 6th-graders. We have also learned how to represent rational numbers using fractions, decimals, and percentages; how to compare and order rational numbers using number lines and equivalent forms; how to perform arithmetic operations with rational numbers using rules and properties; how to solve real-world problems involving rational numbers using strategies and models; how to apply rational numbers in various fields and disciplines; and how to access additional resources for learning and practicing rational numbers online.
You can review and practice what we have learned using Mathskills4kids’ Grade 6 printable worksheets with different problems involving rational numbers. These worksheets will reinforce 6th graders' understanding and skills on rational numbers by providing various questions, examples, and exercises that challenge us to apply what we have learned in different contexts and situations.
You can download these Grade 6 printable worksheets from the links and images above for your students to learn and practice rational numbers confidently at home or independently.
We hope you enjoyed this article on learning and practicing rational numbers for 6th-graders. Happy learning.