Solve and graph equation & inequalities for 6th grade: Worksheets, Tips & Tricks
Hello teachers and parents! Welcome to our article on solving and graphing equations and inequalities in 6th-grade math. We have provided engaging worksheets, tips, and tricks for students to explore and learn these vital math concepts.
-
In this article, your 6th Grade students will learn what inequalities are, how to solve and graph them on a number line, and why they are important for real-world problems. They will also find fun activities to practice inequalities with variables and some challenging questions to test their skills.
Let's get started!
Learn the secrets of solving and graphing inequalities, and practice with these amazing worksheets for 6th-grade
Do you want to help your 6th graders discover and learn the secrets of solving and graphing inequalities? This article is here to help them learn and practice with amazing worksheets from Mathskills4kids.com 6th-grade. Designed by experienced educators and experts, these worksheets are carefully crafted to engage young minds and make learning a joyful experience.
With interactive activities and real-life examples, our worksheets bring the world of equations and inequalities to life, for instance, modeling real-world situations that involve comparisons or limitations.
Let’s dive in and offer students a comprehensive and enjoyable learning experience.
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
Buying is supporting us!
Buy Now...
-
-
What are inequalities in 6th-grade math?
In 6th grade math, inequalities are mathematical statements that compare two expressions using symbols like <, >, ≤, or ≥. For example, 3 < 5 means 3 is less than 5, and 7 ≥ 7 means 7 is greater than or equal to 7.
We can also use a variable, such as x, to represent an unknown number in an inequality. For example, x + 2 > 10 means that whatever number x is, if you add 2 to it, you get a number greater than 10.
-
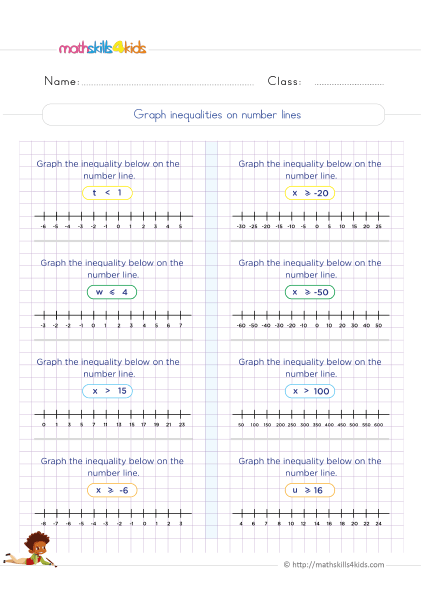
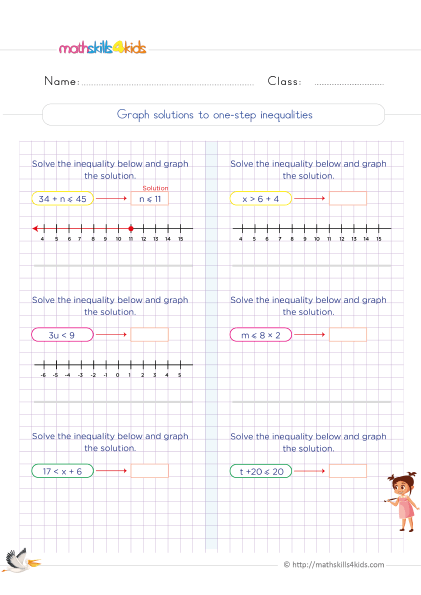
How to solve and graph inequalities on a number line
To solve an inequality, we need to find all the possible values of the variable that make the inequality true. For example, to solve x + 2 > 10, we’ll subtract 2 from both sides of the inequality and get x > 8. This means that any number greater than 8 will make the inequality true.
To graph an inequality on a number line, we need to mark the boundary point (the number that separates the solutions from the non-solutions) with an open circle if the inequality does not include the equal sign (< or >), or with a closed circle if it does (≤ or ≥). Then, we’ll shade the number line part containing the solutions. For example;
To graph x > 8, we need to mark 8 with an open circle and shade the part of the number line to the right of 8.
-
Fun activities to practice inequalities with variables
Apart from worksheets, tips, and tricks, we will provide some fun activities to enhance 6th graders solving inequalities with variables skills.
One way to practice inequalities with variables is to use cards with numbers and symbols. Students can shuffle the cards and deal four cards to each player. Then, each player has to use their cards to make an inequality statement.
For example, if you have cards with 2, x, <, and 9 on them, you can make the statement 2x < 9. The player with the highest value of x wins the round.
Another way to practice inequalities with variables is to use dice and a spinner with symbols on it. You can roll two dice and use them as the numbers in your inequality statement. Then, you can spin the spinner and use the symbol that lands on as the comparison symbol in your statement.
For example, if you roll a 4 and a 6, and the spinner lands on >, you can make the statement 4 > 6. The player with the accurate statement wins the round.
-
Why inequalities are important for real-world problems
There are many reasons why inequalities are important for real-world problems. One such is modeling real-world situations that involve comparisons or limitations. For example, if you want to buy a shirt that costs $15 and have $20 in your pocket, you can write an inequality to represent how much money you will have left after buying the shirt: 20 - 15 ≥ x. This means you will have at least $5 left after buying the shirt.
We can also use inequalities to represent constraints or conditions that must be met. For example, if you want to join a club requiring a grade point average (GPA) of at least 3.5 out of 4.0, you can write an inequality to represent this requirement: GPA ≥ 3.5. This means your GPA must be greater than or equal to 3.5 to join the club.
-
Challenge your 6th-grade students with these 10 inequality questions from Mathskills4kids.com
Are your 6th-grade students ready for some challenge? They can try these 10 inequality questions from Mathskills4kids.com and see how well they understand equations and inequalities.
1) Which inequality is equivalent to -3x + 5 ≤ -13?
- x ≥ -6
- x ≤ -6
- x ≥ -8
- x ≤ -8
2) Which graph represents the solution set of x + 4 > -2?
- A number line with a closed circle at -6 and shading to the left of it.
- A number line with an open circle at -6 and shading to the left of it.
- A number line with a closed circle at -2 and shading to the right of it.
- A number line with an open circle at -2 and shading to the right of it.
3) Which value of x makes the inequality -2x + 7 < -5 true?
- x = -6
- x = 6
- x = -3
- x = 3
4) Which inequality is represented by the graph below?
- x < -4
- x ≤ -4
- x > -4
- x ≥ -4
5) Which inequality describes the situation? You must score at least 80 points on your final exam to pass the course.
- x + 80 ≥ 100
- x - 80 ≥ 100
- 80 + x ≥ 100
- 80 - x ≥ 100
6) Which situation can be modeled by the inequality 3x + 2 ≤ 11?
- You have $11 and want to buy candy bars for $3 each and gum packs for $2 each. How many candy bars and gum packs can you buy?
- You have $11 and want to buy books that cost $3 each and magazines that cost $2 each. How many books and magazines can you buy?
- You have $11 and want to save $3 and spend $2 each week. How many weeks will it take you to save all your money?
- You have $11 and want to earn $3 and spend $2 each week. How many weeks will it take you to spend all your money?
7) Which value of x is a solution of the inequality 2x - 5 > x + 1?
- x = -6
- x = -4
- x = 4
- x = 6
8) Which graph represents the solution set of the compound inequality -2 ≤ x < 5?
- A number line with a closed circle at -2, an open circle at 5, and shading between them.
- A number line with an open circle at -2, a closed circle at 5, and shading between them.
- A number line with a closed circle at -2, an open circle at 5, and shading outside them.
- A number line with an open circle at -2, a closed circle at 5, and shading outside them.
9) Which situation can be modeled by the inequality x/4 + 3 > 5?
- You have $3 and want to buy cupcakes that cost $4 each. How many cupcakes can you buy and still have over $5 left?
- You have $3 and want to sell cupcakes that cost $4 each. How many cupcakes do you need to sell to make more than $5 profit?
- You have 3 hours and want to watch movies lasting 4 hours each. How many movies can you watch and still have over 5 hours left?
- You have 3 hours and want to make movies that last 4 hours each. How many movies do you need to make to use more than 5 hours?
10) Which value of x is not a solution of the inequality |x - 2| < 3?
- x = -1
- x = 0
- x = 1
- x = 5
Review and test student’s solving and graphing equations and inequalities skills in 6th Grade
In this article, your 6th graders have learned much about solving and graphing equations and inequalities. Now, it's time to review and test their skills. Here are some tips to help them:
- To solve an equation, students must find the variable's value that makes both sides of the equation equal. They will use inverse operations (such as addition and subtraction or multiplication and division) to isolate the variable on one side of the equation.
- To solve an inequality, students need to find all the possible values of the variable that make the inequality true. To do this, they must use the same inverse operations as equations but be careful. If someone multiplies or divides both sides of an inequality by a negative number, they must flip the direction of the inequality symbol (< becomes >, or vice versa).
- To graph an equation on a coordinate plane, find two or more points that satisfy the equation (by plugging in different values for the variable), plot them on the plane, and draw a line or a curve that passes through them.
- To graph an inequality on a coordinate plane, graph the corresponding equation first (by replacing the inequality symbol with an equal sign), then shade the region that contains the inequality solutions. If the inequality does not include the equal sign (< or >), use a dashed line or curve for the equation; if it does (≤ or ≥), use a solid line or curve.
Students can also watch videos or play games online that explain equations and inequalities. Here are some links that they can use:
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion
Congratulations! You have reached the end of this article on equations and inequalities. Your 6th graders have learned a lot of new and valuable things that will help them in math and life.
We hope you enjoyed reading this article. We also hope your 6th Grade students had fun with the activities. Remember to encourage them to practice their skills regularly and keep learning more about math.
Thank you for reading!