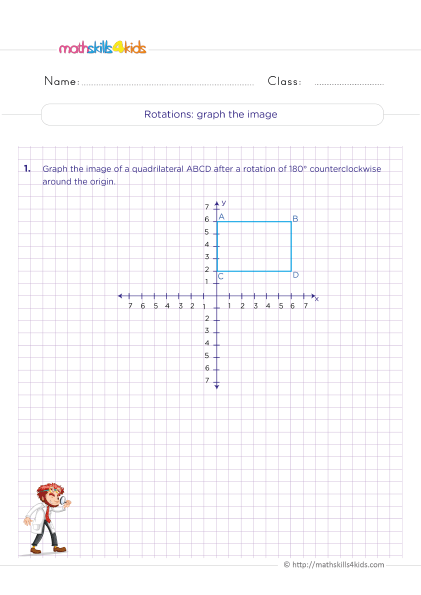
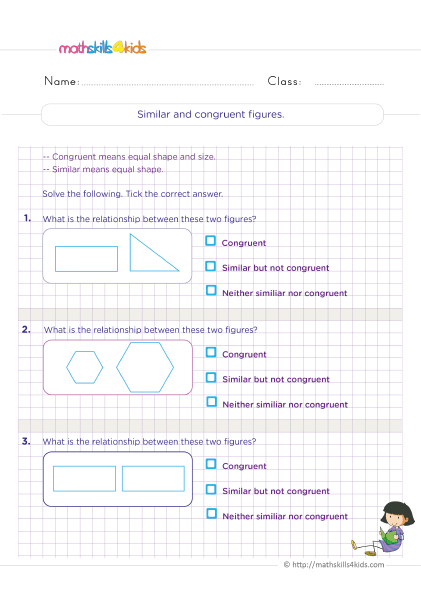
6th Grade symmetry and transformation worksheets
Do you still need help explaining symmetry to your 6th Grade students? If yes. Worry less. In this article, we will share a variety of 6th Grade symmetry and transformation worksheets selected from Mathskills4kids.com that you can download and print for your classroom or home use.
-
In this article, 6th graders will learn the importance of symmetry and transformation in math. Also, they will find simple ways of exploring and identifying types of symmetry, like rotational and lines of symmetry in different shapes and objects.
They will also practice and learn how to create symmetrical patterns using paper folding and cutting, transform shapes using translation, reflection, and rotation, compare congruent and similar figures, and find scale factors. With a few examples, your 6th Grade students will also learn how to apply symmetry and transformation to real-world situations and problems.
As a bonus, we'll show you more websites to download 6th Grade symmetry and transformation worksheets and activities.
So let's get started!
Shape up your 6th Graders’ Math skills with our symmetry and transformation activities.
Are you looking for fun and engaging ways to shape up your 6th Graders’ Math skills? Then you’ve come to the right place! We will provide you with some of our favorite symmetry and transformation activities to help your students develop their spatial reasoning and geometric skills while having a blast.
Whether your child is a visual, auditory, or kinesthetic learner, you will find something here that suits their learning style and goals. So, buckle up, let’s make symmetry and transformation your 6th grader's favorite math topic.
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
GRADE 6 MATH TOPICS
- Whole numbers
- Multiplication
- Division
- Exponents and square roots
- Number theory
- Decimals
- Add & subtract decimals
- Multiply & divide decimals
- Fractions & mixed numbers
- Add & subtract fractions
- Multiply fractions
- Divide fractions
- Integers
- Operations with integers
- Mixed operations
- Rational numbers
- Problems solving
- Ratio & proportions
- Percentages
- Measuring units
- Money math
- Consumer math
- Telling time
- Coordinate graph
- Algebraic expressions
- One step equations
- Solve & graph inequalities
- Two-step equations
- 2D Geometry
- Symmetry & transformation
- 3D Shapes
- Geometry measurement
- Data and Graphs
- Statistics
- Probability
-
Buying is supporting us!
Buy Now...
-
-
What are symmetry and transformation in math, and why are they important?
Symmetry and transformation are two critical topics in math geometry that deal with how shapes and objects can be changed or moved without altering their essential properties. Symmetry means an object can be divided into two or more parts that are exactly the same or mirror images of each other. Transformation means that an object can be moved, flipped, turned, or resized in different ways but still keep its original shape and size.
Symmetry and transformation are important because they help us understand the patterns and structures in nature, art, architecture, design, and many other fields. They also help us solve problems that involve measuring, comparing, drawing, and constructing shapes and figures.
Your 6th graders will improve their visual-spatial skills, logical thinking, and creativity by learning about symmetry and transformation.
-
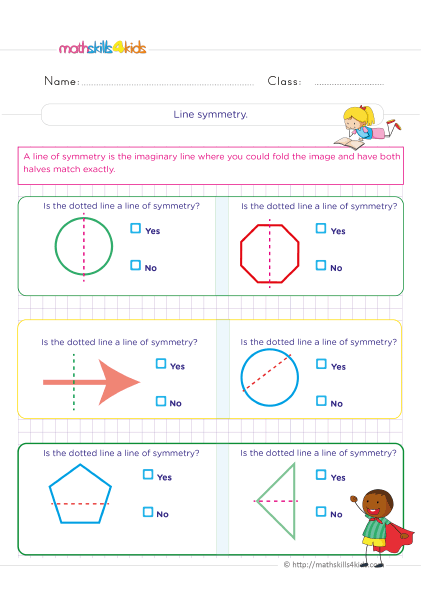
Identifying lines of symmetry in different shapes and objects
One of the simplest ways to introduce symmetry to your students is by showing them how to identify lines of symmetry in different shapes and objects. A line of symmetry is a line that divides an object into two halves that are exactly the same. For example, a square has four lines of symmetry, while a circle has infinitely many.
To practice identifying lines of symmetry, you can use various materials such as paper, cardboard, scissors, rulers, mirrors, stickers, etc. You can ask your students to draw or cut out different shapes and objects and then fold them along their lines of symmetry to check if they match.
You can also use mirrors to reflect one half of an object onto the other and see if they coincide. You can challenge your students to find as many lines of symmetry as possible for each shape or object or to create symmetrical shapes and objects using stickers or other decorations.
-
Creating symmetrical patterns using paper folding and cutting
Another fun activity from Mathskills4kids.com you can do with your students is creating symmetrical patterns using paper folding and cutting. This is a great way to explore the concept of reflection symmetry, which means that an object can be flipped over a line (called the line of reflection) and still look the same.
To create symmetrical patterns using paper folding and cutting, you will need some sheets of paper (preferably colored), scissors, and markers. You can start by folding a sheet of paper in half along a line of symmetry. Then, you can draw a shape or a design on one half of the paper, ensuring it touches the folded edge. Next, you can cut out the shape or design along the drawn lines and unfold the paper. You will get a symmetrical pattern that has two identical halves that are mirror images of each other.
You can repeat this process with different shapes, designs, colors, and paper sizes. You can also experiment with folding the paper more than once along different lines of symmetry before cutting. You can encourage your students to be creative and make different kinds of symmetrical patterns, such as snowflakes, stars, flowers, animals, etc.
-
Exploring rotational symmetry and angle measurement
Another type of symmetry that we can find in shapes and objects is rotational symmetry. This means that we can rotate a shape or an object around a fixed point, and it will look exactly the same as before. The fixed point is called the center of rotation, and the angle we rotate by is called the angle of rotation.
To explore rotational symmetry and angle measurement, we can use a protractor to measure the rotation angles of different shapes and objects. We can also use a compass to draw circles and mark the rotation points. Here are some activities that you can try with your 6th graders:
- Find some shapes and objects with rotational symmetry, such as flowers, snowflakes, pinwheels, logos, etc. Use a protractor to measure their rotation angles and count how many times they match up with themselves in one complete turn. This number is called the order of rotational symmetry.
- Draw a circle on a piece of paper and mark its center. Use a compass to divide the circle into equal parts, such as 4, 6, 8, etc. Cut out the circle and make a small hole in the center. Place the circle on a pencil and spin it around. Observe how the circle looks the same at each point of rotation. You can also decorate the circle with different patterns and colors to make it more fun.
- Cut out some shapes from paper, such as squares, triangles, rectangles, hexagons, etc. Use a pencil to poke a hole in each shape. Place the shape on a pencil and spin it around. Does it have rotational symmetry? If yes, what is its angle and order of rotation? If no, why not? You can also try folding the shape in half or quarters to see if it has line symmetry.
-
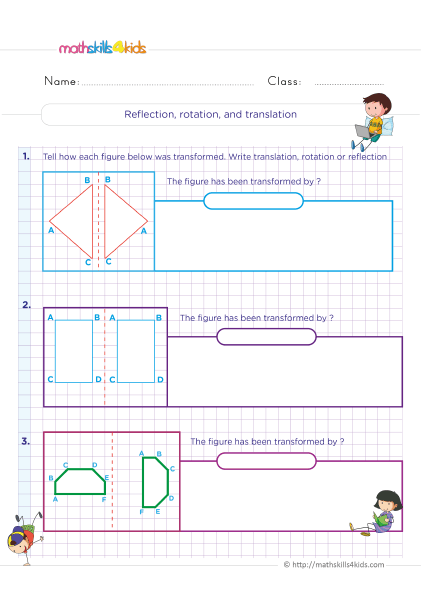
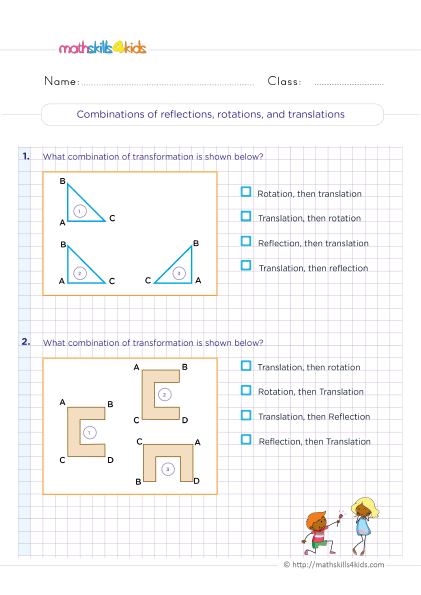
Transforming shapes using translation, reflection, and rotation
Another way that we can change the appearance of shapes is by transforming them using translation, reflection, and rotation. These are called rigid transformations because they do not change the size or shape of the original figure, only its position or orientation.
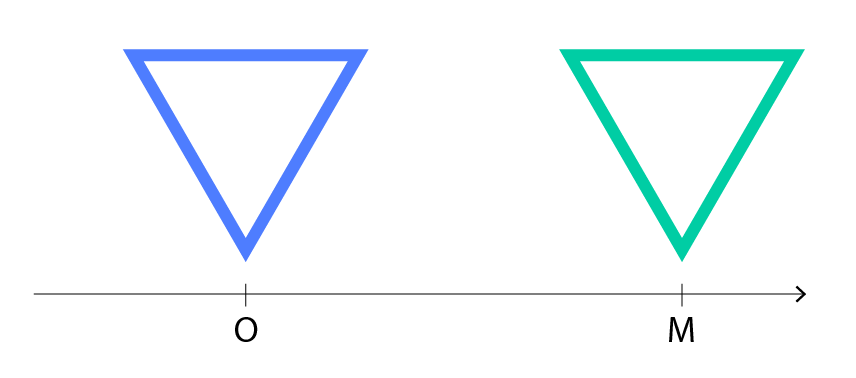
- Translation means moving a shape from one place to another without changing its direction or orientation. For example, we can translate this triangle by sliding it to the right
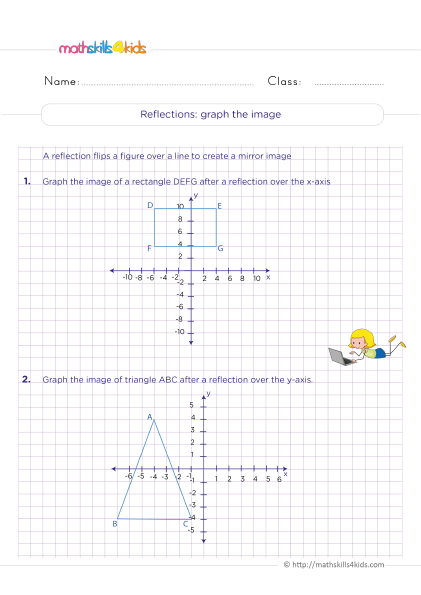
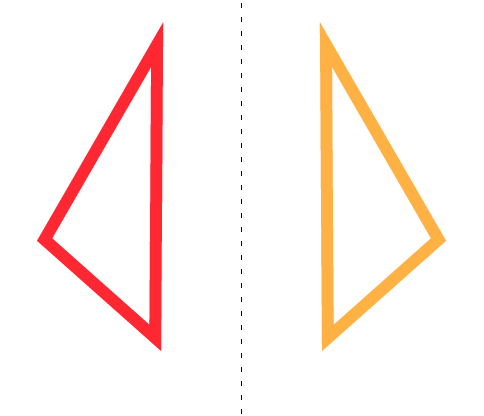
Example of translation - Reflection means flipping a shape over a line of symmetry, called the line of reflection. The shape and its reflection are mirror images of each other. For example, we can reflect this triangle over the vertical line.
Example of reflection - Rotation means turning a shape around a fixed point called the center of rotation. The shape and its rotation are congruent to each other. For example, we can rotate this triangle by 90 degrees clockwise around point O.
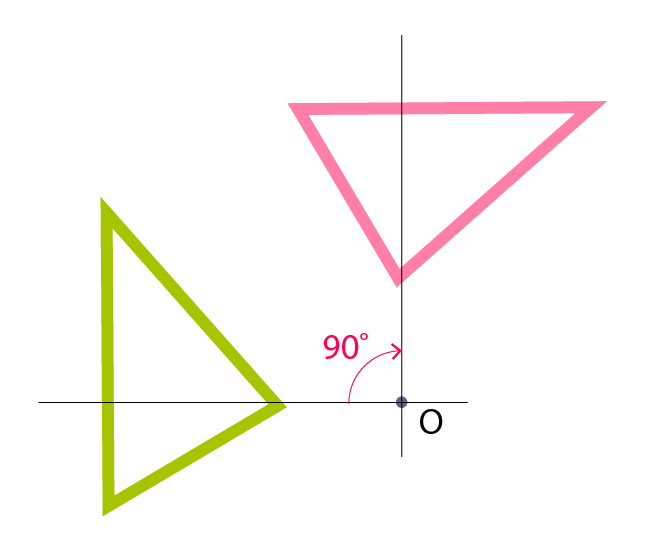
Example of rotation
To practice transforming shapes using translation, reflection, and rotation, we can use graph paper, tracing paper, or geometry software to draw and manipulate different shapes. Here are some activities that you can try with your 6th graders:
- Draw a shape on graph paper and label its vertices with letters. Then draw another shape that is the original shape's translation, reflection, or rotation. Label its vertices with corresponding letters and use arrows to show how the shape was transformed.
- Use tracing paper to trace a shape and then translate, reflect, or rotate it on another piece. Cut out both shapes and compare them. Are they congruent? How do you know? You can also use scissors to cut out shapes from paper and transform them by folding or turning them.
- Use geometry software such as GeoGebra or Sketchpad to create different shapes and transform them using translation, reflection, or rotation tools. You can also explore how changing the transformation parameters affects the resulting shape.
- Translation means moving a shape from one place to another without changing its direction or orientation. For example, we can translate this triangle by sliding it to the right
-
Applying symmetry and transformation to real-world situations and problems
Symmetry and transformation are useful for studying geometry and understanding and solving real-world situations and problems. For example, we can use symmetry and transformation to:
- Create art and design patterns, such as mosaics, mandalas, tessellations, logos, etc.
- Analyze maps and coordinate systems, such as finding locations, distances, directions, etc.
- Explore nature and science, such as finding symmetrical shapes and patterns in plants, animals, crystals, etc.
- Understand physics and engineering, such as balancing forces, rotating objects, scaling models, etc.
We will use our creativity and critical thinking skills to apply symmetry and transformation to real-world situations and problems. We will also use mathematical tools and concepts like measurement, ratio, proportion, algebra, etc.
Here are some activities that you can try with your 6th graders:
- Create your own art or design project using symmetry and transformation. You can use paper, scissors, glue, colors, etc., to make symmetrical patterns or shapes. You can also use geometry software or online tools to create digital art or design. Explain how you used symmetry and transformation in your project.
- Use a map of your city or country to practice using coordinates and transformations. You can use graph paper or online tools to draw a coordinate grid on the map. Then you can plot points on the map using coordinates and transform them using translation, reflection, or rotation. Using measurement and angle tools, you can also find distances and directions between points.
- Find some examples of symmetry and transformation in nature or science. You can use books, magazines, websites, or videos to research different topics such as biology, chemistry, astronomy, etc. You can also observe your surroundings and look for symmetrical shapes or patterns in plants, animals, or objects. Explain how symmetry and transformation help you understand these topics better.
- Solve some problems that involve physics or engineering using symmetry and transformation. You can use books, magazines, websites, or videos to find problems that interest you, such as building bridges, launching rockets, flying planes, etc. You can also make your problems using everyday objects or situations. Explain how you used symmetry and transformation to solve these problems.
Bonus: Where to find more resources to reinforce 6th graders' symmetry and transformation skills
If you and your students enjoyed these 6th Grade symmetry and transformation worksheets and activities and want to learn more, here are some web links with descriptions that you can explore:
- https://www.mathsisfun.com/geometry/symmetry.html: This website explains the concept of symmetry simply and interactively. Your students can learn about different types of symmetry, such as reflection, rotation, translation, and glide reflection. They can also play with online tools to create symmetrical designs and patterns.
- https://www.mathplayground.com/shape_transformations.html: This website lets students practice transforming shapes using translation, reflection, and rotation. They can drag and drop the shapes to match the images or create transformations using the arrows and buttons. They can also adjust the level of difficulty and the grid size.
- https://www.khanacademy.org/math/cc-sixth-grade-math/cc-6th-geometry-topic/cc-6th-symmetry/v/line-of-symmetry: This website offers a video lesson on how to identify lines of symmetry in different shapes and objects. Students can also take a quiz to test their understanding and get feedback on their answers.
- https://www.mathworksheets4kids.com/symmetry.php: This website provides a variety of printable worksheets on symmetry for different grade levels. Students can choose from topics such as drawing lines of symmetry, completing symmetrical figures, identifying symmetrical shapes, finding rotational symmetry, and more. They can also download the answer keys for each worksheet.
-
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
Conclusion: Summarizing the main points and giving some tips for further practice
In this article, we have learned about symmetry and transformation in math and why they are essential. We have also explored fun and engaging activities to help 6th graders develop symmetry and transformation skills. Here are some key points to remember:
- Symmetry is when one shape becomes exactly like another when you move it in a certain way. Different types of symmetry exist, such as reflection, rotation, translation, and glide reflection.
- Transformation is changing a shape's position, size, or orientation. There are three fundamental transformations: translation (sliding), reflection (flipping), and rotation (turning).
- Congruent figures are figures that have the same size and shape. Similar figures have the same shape but not necessarily the same size. The scale factor is the ratio of the lengths of corresponding sides of similar figures.
- Symmetry and transformation are useful in math and beyond. They help us understand patterns, shapes, angles, measurements, proportions, etc. They also help us appreciate the beauty and order of nature, art, architecture, and design.
To help 6th graders further practice their symmetry and transformation skills, they can try some of these tips:
- Look for examples of symmetry and transformation in the surroundings. For instance, we can find lines of symmetry in leaves, flowers, butterflies, flags, logos, etc. We can also find transformations in maps, puzzles, games, animations, etc.
- Use different materials and tools to create symmetrical patterns and designs. For example, we can use paper folding and cutting, origami, kaleidoscopes, mirrors, tracing paper, etc.
- Challenge themselves with some puzzles and problems that involve symmetry and transformation. For example, students can try to find the missing pieces of a symmetrical figure or figure out how to transform one shape into another using the least number of moves.
We hope you and your 6th graders have enjoyed this article and learned something new about symmetry and transformation. Remember to have fun with math and keep exploring!