Learn the facts and tricks of divisibility rules: 3rd Grade worksheets
Welcome to another amazing math resource where we aim to make teaching and learning math a beautiful experience for teachers, parents, and children. Today, we will discuss another important strategy for building on 3rd graders' division skills: Divisibility rules. After going through this article, don't hesitate to download our 3rd Grade division worksheets from Mathskils4kids.com and help your 3rd graders learn the facts and tricks of divisibility rules.
You can also print and use these worksheets for free with your children at home or in the classroom as extra practice.
-
In this article, you will learn about divisibility rules and their importance. You will also learn to use them for different numbers, from 2 to 12. You will discover some fun tricks and tips to remember them easily. And you will get to practice them with our free worksheets that you can download at the end of this article.
In addition, you will see some real-world examples of how divisibility rules can help you in everyday life. And as a bonus, we will share some more resources and activities that you can use to reinforce your division skills at home and school.
So, are you ready to become a division master? Let's get started!
What are divisibility rules, and why are they important?
As a teacher or parent, begin by helping your 3rd graders understand divisibility rules and why they are important before discovering how they work.
Divisibility rules are shortcuts that help you find out if a number can be divided by another number without doing long division. For example, if you want to know if 24 can be divided by 4, you can use a divisibility rule instead of dividing 24 by 4. Divisibility rules can save you time and make division easier.
Divisibility rules are also important because they help you understand the properties of numbers and how they relate. For example, if you know that a number is divisible by 2, you will also know that it is an even number. If you know that a number is divisible by 3, then you also know that the sum of its digits is divisible by 3. Divisibility rules can help you develop number sense and algebraic thinking.
Divisibility rules also help us to find the factors of numbers. Factors are numbers that divide another number evenly. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Knowing the factors of numbers can help us to simplify fractions, find common multiples, and do other math operations.
-
BROWSE THE WEBSITE
-
DOWNLOAD FREE WORKSHEETS
-
-
3rd GRADE MATH TOPICS
- Number and compapring
- Place value
- Addition
- Subtraction
- Understand multiplication
- Multiplication skill builders
- Multiplication fluency
- Multiplication
- Understand division
- Division skill builders
- Division fluency
- Division practice
- Mixed operation
- Properties
- Equations & variations
- Estimate & rounding
- Logical reasoning
- Patterns
- Money
- Telling time
- Data graph & probability
- Understanding fractions
- Equivalent fractions
- Comparing and ordering fractions
- Operations with fractions
- Unit of measurement
- Two-dimensional shapes
- Triangles and quadrilaterals
- 3D shapes
- Geometric measurement
-
Buying is supporting us!
Buy Now...
-
-
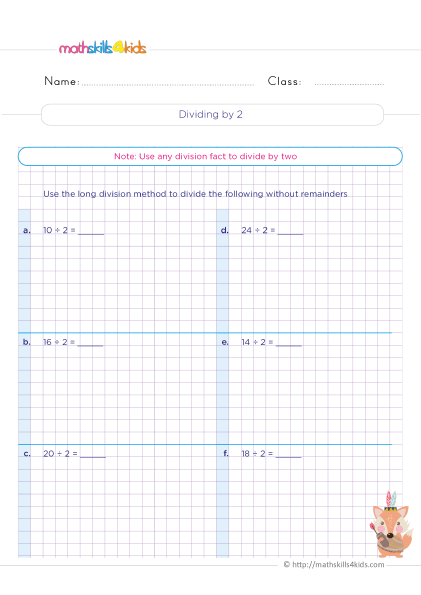
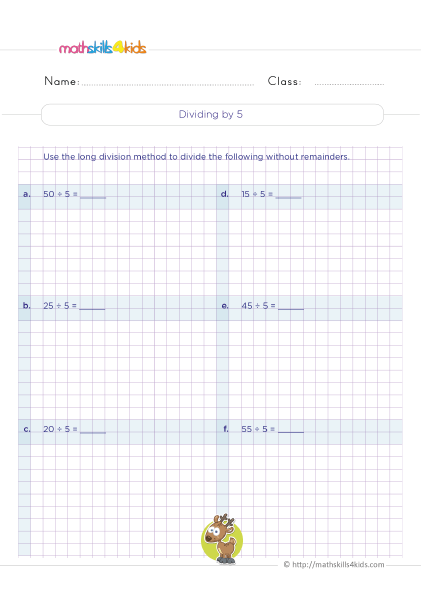
How to use the divisibility rule for 2, 5 and 10
The divisibility rule for 2, 5, and 10 is easy and useful. It helps you quickly check if a number can be divided by 2, 5, or 10 without doing any calculations. Here's how it works:
- A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
- A number is divisible by 5 if its last digit is 0 or 5.
- A number is divisible by 10 if its last digit is 0.
For example, let's look at the number 450. Its last digit is 0, so it is divisible by 2, 5, and 10. You can easily confirm this by dividing it by each of these numbers and getting a whole number as the answer:
- 450 ÷ 2 = 225
- 450 ÷ 5 = 90
- 450 ÷ 10 = 45
Now let's look at another number: 357. Its last digit is 7, which is odd, not 0 or 5. So it is not divisible by 2, 5, or 10. You can also verify this by trying to divide it by each of these numbers and getting a decimal or a remainder as the answer:
- 357 ÷ 2 = 178.5
- 357 ÷ 5 = 71.4
- 357 ÷ 10 = 35.7
You can use this rule to quickly test any number for divisibility by 2, 5, or 10. It's a great way to save time and mental energy when doing division problems.
-
How to use the divisibility rule for 3 and 9
The divisibility rule for 3 and 9 is more tricky than the one for 2, 5, and 10, but it's still handy and fun. It helps you check if a number can be divided by 3 or 9 by looking at the sum of its digits. Here's how it works:
- A number is divisible by 3 if the sum of its digits is divisible by 3.
- A number is divisible by 9 if the sum of its digits is divisible by 9.
For example, let's look at the number 729. To find the sum of its digits, we add them up:
`7 + `2 + `9 = `18
The sum of the digits is `18`, divisible by `3` and `9`. So we can conclude that `729` is also divisible by `3` and `9`. We can check this by dividing it by each of these numbers and getting a whole number as the answer:
`729` ÷ `3` = `243`
`729` ÷ `9` = `81`
-
Now let's look at another number: `532`. To find the sum of its digits, we add them up:
`5 + `3 + `2 = `10
The sum of the digits is `10`, which is not divisible by either `3` or `9`. So we can conclude that `532` is not divisible by `3` or `9`.
You can use this rule to quickly test any number for divisibility by `3` or `9`. It's a good way to practice your addition and mental math skills.
-
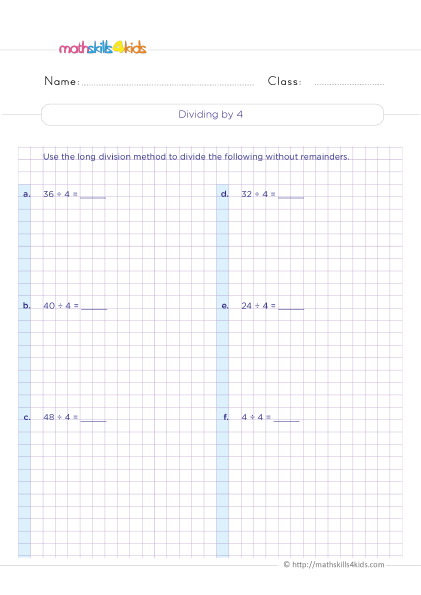
How to use the divisibility rule for `4` and `8`
The divisibility rule for `4` and `8` is similar to the one for `2`, but it involves looking at the last two digits instead of just the last one. It helps you check if a number can be divided by `4` or `8` by looking at whether the last two digits form a number divisible by `4` or `8`. Here's how it works:
- A number is divisible by `4` if its last two digits are divisible by `4`.
- A number is divisible by `8` if its last three digits are divisible by `8`.
For example, let's look at the number `1236`. To check if it is divisible by `4`, we look at its last two digits: `36`. `36` is divisible by `4`, so we can conclude that `1236` is also divisible by `4`. We can confirm this by dividing it by `4` and getting a whole number as the answer:
`1236` ÷ `4` = `309`
To check if it is divisible by `8`, we look at its last three digits: `236`. `236` is not divisible by `8`, so we can conclude that `1236` is not divisible by `8`. We can also verify this by trying to divide it by `8` and getting a decimal or a remainder as the answer:
`1236` ÷ `8` = `154.5`
Now let's look at another number: `4096`. To check if it is divisible by `4`, we look at its last two digits: `96`. `96` is divisible by `4`, so we can conclude that `4096` is also divisible by `4`. We can check this by dividing it by `4` and getting a whole number as the answer:
`4096` ÷ `4` = `1024`
To check if it is divisible by `8`, we look at its last three digits: `096`. `096` is divisible by `8`, so we can conclude that `4096` is also divisible by `8`. We can check this by dividing it by `8` and getting a whole number as the answer:
`4096` ÷ `8` = `512`
You can use this rule to test any number for divisibility by 4 or 8. It's a useful way to improve your division skills and number sense.
-
How to use the divisibility rule for 6 and 12
You will notice that the divisibility rules for 6 and 12 are related to the rules for 2 and 3. That's because 6 is the product of 2 and 3, and 12 is the product of 2 and 2 and 3. So, to check if a number is divisible by 6, check if it is divisible by 2 and 3. And to check if a number is divisible by 12, you need to check if it is divisible by both 4 and 3. Here are some examples:
- Is 48 divisible by 6? Yes, because it is divisible by both 2 (it ends in an even digit) and 3 (the sum of its digits is 12, which is divisible by 3).
- Is 72 divisible by 12? Yes, because it is divisible by both 4 (the last two digits form a number divisible by 4) and 3 (the sum of its digits is 9, which is divisible by 3).
- Is 63 divisible by 6? No, because it is not divisible by 2 (it ends in an odd digit).
- Is 64 divisible by 12? No, because it is not divisible by 4 (the last two digits form a number not divisible by 4).
-
Fun tips to learn the facts and tricks of divisibility rules: Best Mathskills4kids 3rd Grade worksheets
Now that you have learned the basic divisibility rules for the most common factors, you might be wondering how to remember them all. Don't worry. Our Mathskills4kids 3rd Grade worksheets have designed fun tips to learn the facts and tricks of divisibility rules and remember them always.
They include:
- For the divisibility rule for 2, you can think of a rhyme: If it ends in zero or an even number, then it's divisible by two - no wonder!
- For the divisibility rule for 3, you can think of a song: Add up all the digits and see if they're divisible by three - yippee!
- For the divisibility rule for 4, you can think of a word: Look at the last two digits - that's the key if they're divisible by four - easy peasy!
- For the divisibility rule for 5, you can think of a gesture: Hold up your hand and count your fingers - one, two, three, four, five. If it ends in zero or five - high five!
- For the divisibility rule for 6, you can think of a rule: If it's divisible by two and three - then it's also divisible by six - easy breezy!
- For the divisibility rule for 8, you can think of a trick: Cut off the last three digits and see if they're divisible by eight - great!
- For the divisibility rule for 9, you can think of a game: Add up all the digits and see if they're divisible by nine - fine!
- For the divisibility rule for 10, you can think of a fact: If it ends in zero - then it's divisible by ten - super!
-
Real-world examples of using divisibility rules in everyday life
You might be wondering why you need to learn divisibility rules. After all, you can always use a calculator or long division to find out if a number is divisible by another number. Well, divisibility rules are not only useful for math class. They can also help you in everyday situations where you will divide or simplify numbers quickly.
Here are some real-world examples of using divisibility rules:
- Suppose you want to split a pizza among your friends. You can use the divisibility rule for 2 to check if the number of slices is even or odd. If it's even, you can divide it equally among your friends. If it's odd, you can cut one slice in half or leave one for yourself.
- Suppose you want to buy some candy bars at the store. You can use the divisibility rule for 3 to check if the price of each candy bar is a multiple of three. If it is, pay with a dollar bill and get no change. If not, buy more candy bars or pay with coins.
- Suppose you want to arrange some books on a shelf. You can use the divisibility rule for 4 to check if the number of books is a multiple of four. If it is, you can arrange them in rows of four. If it's not, you can leave some space on the shelf or stack some books on each other.
- Suppose you want to tip a waiter at a restaurant. You can use the divisibility rule for 5 to check if the bill amount is a multiple of five. If it is, you can tip 20% by moving the decimal point one place to the left and doubling the result. If not, you can either round up or down the bill amount to the nearest multiple of five and then tip 20%.
Bonus: More resources and activities to reinforce division skills at home and school
If you want to learn more about division and the facts and tricks of divisibility rules, we have more resources, activities, and 3rd Grade worksheets to explore. You can use them to reinforce your division skills at home and school. Here are some suggestions:
- Watch this video that explains the divisibility rules in a fun and easy way: https://www.youtube.com/watch?v=JjREbnseM1U
- Play this online game that tests your knowledge of divisibility rules: https://www.mathplayground.com/divisibility_rules.html
- Read this book that teaches you how to use divisibility rules to solve math problems: The Best of Times: Math Strategies that Multiply by Greg Tang
- Try this challenge that asks you to find all the numbers from 1 to 100 that are divisible by a given factor: https://www.pinterest.com/pin/divisibility-rules-help-us-figure-out-if-a-number-is-divisible-by-2-3-4-5-9-10-25-and-100--155514993373011461/
-
Thank you for sharing the links of MathSkills4Kids.com with your loved ones. Your choice is greatly appreciated.
We hope you enjoyed this article and learned something new about divisibility rules. Divisibility rules are not only fun and easy to learn but also useful and practical in everyday life.
They can help you divide and simplify numbers quickly and accurately. They can also help you develop your number sense and mental math skills.
So, remember to practice them regularly and apply them whenever you can. And, of course, Mathskills4kids.com is your most reliable website where you can learn the facts and tricks of divisibility rules through their 3rd Grade worksheets. Have fun and enjoy learning!
Happy dividing!